A Note on the Toughness and Edge-Toughness of Kronecker Product of Graphs?

Raxida Guji

(1.Center for Discrete Mathematics,Fuzhou University,Fuzhou Fujian 350002,China

2.School of Applied Mathematics,Xinjiang University of Finance and Economics,Urumqi Xinjiang 830012,China;)

0 Introduction

Throughout this paper we consider only f i nite,connected and undirected graphs without loops and multiple edges.LetG=(V,E)be a graph with vertex setV=V(G)and edge setE=E(G).We denote by bxc the greatest integer not exceeding a real numberx.For notation and terminology not def i ned here we refer to West[1].

The toughnesst(G)of a noncomplete graphGis def i ned ast(G)=min{|S|/ω(G?S)|S?V(G),ω(G?S)≥2},where ω(G?S)is the number of connected components ofG?S,andt(G):=∞ifGis a complete graph.The toughness of a graph is an invariant f i rst introduced by Chv′atal[2].He observed some relationships between this parameter and existence of hamiltonian cycles or k-factors.More recently,toughness has also been considered as a vulnerability measure for networks,since it measures how badly a graph breaks up in components when a set of vertices is removed.Unfortunately,this measure is difficult to calculate as shown by Bauer et al.[3]that it isNP-hard to determine the toughness of a graph.

Since this parameter was introduced,a lot of research has been done,mainly relating toughness conditions to the existence of cycle structures.However,exact values oft(G)are known only for a few families of graphsG,such as paths and cycles[4],the Catersian product of two complete graphs[2]and of paths and cycles[5],and the composition of two graphs,one of them being a path,a cycle or a complete bipartite graph[5],the Kronecker product of two complete graphs[6],the Kronecker product of a complete graph and a path,a star,respectively,the sharp upper and lower bounds for Kronecker product of a complete graph and a tree[7].

A subsetXofE(G)is called an edge-cutset if ω(G?X)>1.The edge-toughnesst0(G)ofGis def i ned asis an edge-cut set ofG}.This concept is introduced by Peng et al.[8],motivated by the following theorem discovered independently by Tutte[9]and Nash-Williams[10].

Theorem 1A connected graphGhas s edge-disjoint spanning trees if and only if|X|≥s(ω(G?X)?1)for every subsetXofE(G).

The area of graph vulnerability concerns the question of how much communication in a network is disrupted by the deletion of edges from the graph.The most fundamental measure of graph vulnerability of a connected graph is the edge-connectivity of the graph.One of the motivations in studying the edge-toughness of a graph is that it can be used as a more ref i ned measure of graph vulnerability than that based on simple edge-connectivity[11].The smaller the edge-toughness,the more vulnerable is the graph,in the sense that more components will be created by fewer edge deletions.The edge-toughness becomes a more signif i cant measurement in comparing the vulnerability of two graphs when they have the same edge-connectivity.

The Kronecker product(also named direct product,tensor product and cross product)G1×G2is def i ned as:V(G1×G2)=V(G1)×V(G2)andE(G1×G2)={(u1,v1)(u2,v2):u1u2∈E(G1)andv1v2∈E(G2)}.The Kronecker product of graphs has been extensively investigated concerning graph colorings,graph recognition and decomposition,graph embeddings,matching theory and stability in graphs(see,for example[12]and[13],and the references therein),and this graph product has several applications,for instance it can be used in modeling concurrency in multiprocessor system[14]and in automata theory[15].

In this paper,we study toughness and edge-toughness of Kronecker product of some special graphs.In section 2,we determine the toughness of Kronecker product of a complete graph and a cycle.In section 3,we investigate the edge-toughness of Kronecker product of a complete graph and regular graphs.

We conclude this section by listing some known properties and results on the toughness of Kronecker product of graphs.

Theorem 2[6]Letmandnbe integers withn≥m≥2 andn≥3.Thent(Km×Kn)=m?1.

Theorem 3[7]LetTbe a non-trivial tree andn≥3.Then

Theorem 4[7]Letmandnbe integers withn≥m≥2 andn≥3,and letPmbe a path withmvertices.Then

Proposition 1[16]LetH=G1×G2=(V(H),E(H)).Then

(1)|V(H)|=|V(G1)|·|V(G2)|,

(2)|E(H)|=2|E(G1)|·|E(G2)|,

(3)for every(u,v)∈V(H),degH((u,v))=degG1(u)·degG2(v).

1 Toughness

We start with our main result on the toughness ofCm×Kn.

Theorem 5Letmandnbe integers withn≥m≥3,and letCmbe a cycle withmvertices.Then

Before starting the proof of our main result in the section,we introduce some notations for later use.

When considering the Kronecker product of a graphGandKn,we shall always labelV(G)={u1,...,um},V(Kn)={v1,...,vn}and setSi={ui}×V(Kn),i=1,2,···,m.Moreover,for convenience,we shall abbreviate(ui,vj)aswijfori=1,2,···,mandj=1,2,···,n.ThenSi={wi1,wi2,···,win},i=1,2,···,m,are independent sets inG×Kn,andV(G×Kn)has a partitionV(G×Kn)=S1∪S2∪···∪Sm.

A vertex cutSof a noncomplete connected graphGis said to be optimal,

Following lemmas play a key role in the proof of Theorem 5.

In view of Lemma 1,we may assume thatS∩Si=SiorS∩Si= ?for somei∈ {1,2,···,m}for every optimal cut setSofPm×Kn.

Lemma 2LetSbe a vertex cut ofG=Cm×Kn(m≥4,n≥3).IfS∩Si,?andS∩Si,Sifor somei∈{1,2,···,m},thenSis not optimal.

Case 1|S∩S1|=n?2.

But then,by setting a cut setS0=S1∪S3∪···Sm?1,we have

Case 2|S∩S1|=n?1.

Case 3|S∩S1|=n.

SinceG?S1?Pm?1×Kn,by Lemma 1 we get the result.

Now we are ready to give the proof of Theorem 5.

Proof of Theorem 5We f i rst determine the toughness ofC3×Knforn≥3.

By Theorem 2,t(C3×Kn)=t(K3×Kn)=2.

In the rest of this proof letm≥4 andn≥3.By Lemma 2,we may assume that every optimal vertex cutSofGhas the formS=∪i∈ISifor someI?{1,2,...m}.

Claim 1LetSbe a vertex cut ofG=Cm×Kn(m≥4,n≥ 3).IfSi,Si+1,Si+2?Sfor somei∈{1,2,···,m?1},thenSis not optimal.

LetSbe a vertex cut ofG=Cm×Kn(m≥4,n≥3).IfSi,Si+1,Si+2?Sfor somei∈{1,2,···,m?1},then we setS0=SSi+1.Note that|S0|=|S|?nand ω(G?S0)=ω(G?S)+n.Thus,we have proved.

Claim 2LetSbe a cut set ofG=Cm×Kn(m≥4,n≥3).Suppose that there existiandksuch thatSi,Si+k?SandS∩Sj=?fori+1≤j≤i+k?1,i∈{1,...,m?k}.Ifk≥3,thenSis not an optimal vertex cut ofG.

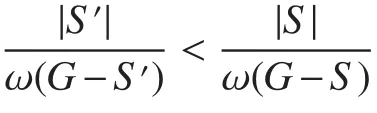
Claim 3There exists an optimal vertex cutSofGfor which there exists noj>i+2(i,j∈ {1,2,···,m?1})withSi,Si+1?SandSj,Sj+1?S.

Suppose there exists an optimal vertex cutSofGfor which there existsj>i+2(i,j∈ {1,2,···,m?1})withSi,Si+1?SandSj,Sj+1?S.By Claim 2,we may assume thatj=i+3 orj=i+5 andSi+3?S.

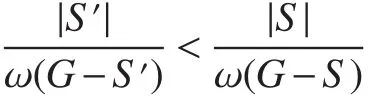
2 Edge-toughness

In this section,we shall f i nd the edge-toughness of some Kronecker product of graphs.We shall f i rst recall following theorems.

Theorem 7[18]For any graphGandn≥3,κ0(G×Kn)=min{n(n?1)κ0(G),(n?1)δ(G)}.

By Theorem 6 and Theorem 7,we have

The following corollary is immediate.

References：

[1]West D B.Introduction to Graph Theory(2nd Edition)[M].NJ Upper Saddle River:Prentice Hall,2001.

[2]Chv′atal V.Tough graphs and Hamiltonian circuits[J].Discrete Math,1973,5:215-228.

[3]Bauer D,Morgana A,Schmeichel E.On the complexity of recognizing tough graphs[J].Discrete Math,1994,124:13-17.

[4]Pippert R E.On the toughness of a graph[J].Lecture Notes in Math,1972,303:225-233.

[5]Goddard W D,Swart H C.On the toughness of a graph[J].Quasstiones Mathematics,1990,13:217-232.

[6]Mamut A,Vumar E.Vertex vulnerability parameters of Kronecker product of complete graphs[J].Inform Process Lett,2008,106:258-262.

[7]Guji R,Ali T.Toughness of Kronecker products of graphs[J].Ars Combin,2016,127:149-156.

[8]Peng Y H,Chen C C,Koh K M.On the edge-toughness of a graph(1)[J].Southeast Asian Math Bull,1988,12:109-122.

[9]Tutte W T.On the problem of decomposing a graph into n connected factors[J].London Math Soc,1961,36:221-230.

[10]Nash-Williams C St J A.Edge-disjoint spanning trees of f i nite graphs[J].J London Math Soc,1961,36:445-450.

[11]Gusf i eld D.Connectivity and edge-disjoint spanning trees[J].Inform Process Lett,1983,16:87-89.

[12]Alon N,Lubetzky E.Independent sets in tensor graph powers[J].J Graph Theory,2007,54:73-87.

[13]Breˇsar B,Imrich W,Klavˇzar S,et al.Hypercubes as direct products[J].SIAM J Discrete Math,2005,18:778-786.

[14]Lammprey R H,Barnes B H.Products of graphs and applications[J].Modeling and Simulation,1974,5:1119-1123.

[15]Ghozati S A.A f i nite automata approach to modeling the cross product of interconnection networks[J].Mathematical and Computer Modeling,1999,30:185-200.

[16]Bottreou A,M′etivier Y.Some remarks on the Kronecker product of graphs[J].Inform Process Lett,1998,68:55-61.

[17]Peng Y H,Tay T S.On the edge-toughness of a graph(2)[J].J Graph Theory,1993,17:233-246．

[18]Cao X L,Brglez?S,?Spacapan S,et al.On edge connectivity of direct products of graphs[J].Inform Process Lett,2011,111:889-902.