Effect of channel shape on selection of time marching scheme in the discontinuous Galerkin method for 1-D open channel flow*

SAFARZADEH MALEKI Farzam, KHAN Abdul A.

1. Engineering Department, Massachusetts Maritime Academy, Buzzards Bay, MA 02532, USA, E-mail:fmaleki@maritime.edu

2. Glenn Department of Civil Engineering, Clemson University, Clemson, SC 29634, USA

Effect of channel shape on selection of time marching scheme in the discontinuous Galerkin method for 1-D open channel flow*

SAFARZADEH MALEKI Farzam1, KHAN Abdul A.2

1. Engineering Department, Massachusetts Maritime Academy, Buzzards Bay, MA 02532, USA, E-mail:fmaleki@maritime.edu

2. Glenn Department of Civil Engineering, Clemson University, Clemson, SC 29634, USA

(Received June 27, 2014, Revised November 26, 2014)

One-dimensional open channel flows are simulated using the discontinuous Galerkin finite element method. Three different explicit time marching schemes, including multistep/multistage schemes, are evaluated for different channel shapes for accuracy and efficiency. The Forward Euler, second-order Adam-Bashforth (multistep), and second-order total variation diminishing (TVD) Runge-Kutta (multistage) time marching schemes are utilized. The role of monotonized central, minmod, and zero TVD slope limiters for each of the time marching scheme is investigated. The numerical flux is approximated using HLL function. The accuracy and robustness of different time marching schemes are evaluated for steady and unsteady flows using analytical and measured data. The unsteady flows include dam break tests with wet and dry beds downstream of the dam in prismatic (rectangular, trapezoidal, triangular, and parabolic cross-sections) and non-prismatic (natural river) channels. The steady flow test involves simulation of hydraulic jump in a diverging rectangular channel. The various schemes are evaluated by comparing accuracy using statistical measures and efficiency using maximum possible time step size as well as CPU runtime. The second-order Adam-Bashforth time marching scheme is found to have the best accuracy and efficiency among the time stepping schemes tested.

discontinuous Galerkin method, shallow water equations, time marching schemes, total variation diminishing (TVD) slope limiter

Introduction

Shallow water flow equations, also known as Saint-Venant equations, are widely used in hydraulic and river engineering problems. Many researchers, with the use of different numerical methods such as finite volume, finite difference, and finite elements, have tried to numerically solve these equations[1-3]. In recent years, the discontinuous Galerkin (DG) finite element method, which is a modified version of the traditional (continuous) Galerkin finite element method, has gained popularity in numerical modeling of shallow water flows[4-8]. The continuous Galerkin finite element methods are usually unsatisfactory, due to oscillations near shocks, in dealing with advectiondominated flows[7]. The DG method combines the desirable properties of finite element and finite volume methods[7], and is capable of observing conservation properties[9]. Various upwinding schemes can be easily implement through the discontinuous element boundaries. In addition,P -adaptivity and h-adaptivity can be easily implemented in this method[10].

In solving hyperbolic equations, exact or approximate solution of the Riemann problem is required for accurate representation of the numerical flux. Since exact solution of the Riemann problem is generally considered too expensive for most problems, several approximate Riemann solvers have been developed. The most commonly used approximate Reimann solvers in recent studies are HLL, HLLE, and HLLC. In addition to the flux approximation, appropriate treatment of the source term is critical for preserving the conservation properties and achieving a well-balanced scheme[5]. Recently, Hubbard and Garcia-Navarro[11]proposed a scheme that balanced sourceterms and flux gradients; the upwind method of Bermudez and Vázquez[12]was used for discretizing the source terms. Ying et al.[13]approximated the water surface gradient (treated as a part of the source term) as a weighted average of upwind and downwind water surface gradients based on the local Courant number, while the friction was computed assuming the variables to be piecewise constant.

Generally, slope limiters are used in order to circumvent numerical oscillations in the computed results. Use of slope limiters, together with an appropriate high resolution scheme, makes the solutions total variation diminishing (TVD). Spurious oscillations near discontinuities and in areas of high gradients reveal the importance of stabilization techniques such as slope limiters[14]. According to Li[9], the way the element boundary fluxes are computed determines the spatial order of accuracy of the numerical algorithm and controls the amplitude of local jumps at an element interface. If these jumps are monotonically reduced, the scheme provides more accurate initial guesses for the solution of the local Riemann problems (the average values give only the first-order accuracy). Hassanzadeh et al.[15]conducted a comparative study to find appropriate flux limiters for the one-dimensional gas-solid reactive flow simulations using finite difference method. However, the performance of different TVD slope limiters for the shallow water flow modeling using the DG method has not been evaluated.

Spatial and temporal discretizations are important for the stability requirement and accuracy of a scheme. Over the past few decades, many efforts have been made to achieve accurate and efficient time marching schemes. Time integration schemes include single step, multistep, and multistage methods. Multistep methods, such as Adam-Bashforth (AB), attempt to gain efficiency and accuracy by keeping and using the information from previous time steps rather than discarding it. In addition, a desirable feature of a multistep method is that the local truncation error can be determined and a correction term can be included, which improves the accuracy of the results at each time step[16]. In multistage methods, such as Runge-Kutta, intermediate values have to be calculated to progress the solution from one time step to the other. Forward Euler (FE) constitutes the simplest time marching scheme and may be considered as the lowest order Runge-Kutta or AB scheme.

To achieve a stable scheme in the DG method, TVD Runge-Kutta time discretization schemes have been used widely, especially the second-order TVD Runge-Kutta scheme[17]. Despite its common use, the efficiency and accuracy of the second-order TVD Runge-Kutta scheme in the DG framework, while using a TVD slope limiter, has not been compared to other time stepping schemes. In addition, the role of channel geometry in the selection of a suitable time marching scheme has not been investigated.

The aim of this paper is to evaluate the performance (efficiency and accuracy) of multistage and multistep time marching schemes in the DG framework and to investigate how the channel geometry dictates the selection of a time marching scheme. The time marching schemes that are evaluated include second-order TVD Runge-Kutta, FE, and second-order AB schemes. Secondly, monotonized central (MC), minmod, and zero slope limiters are examined for each of the time marching scheme. The performance of a slope limiter is evaluated based on its TVD property and diffusion control.

1. Model formulation

1.1 Governing equations

The general form of the governing equations of one dimensional shallow water flow is given by Eq.(1), whereU,F( U), and S( U)are, respectively, the vectors of conserved variables, flux terms, and source terms, and are defined using Eq.(2). In Eq.(2),A,Q, gand Soare cross section area, volumetric flow rate, gravitational acceleration, and bed slope, respectively. The hydrostatic pressure force,I1, the wall pressure force,I2, the energy slope,Sf, and the bed slope,So, are defined using Eqs.(3) and (4). In these equations, R,b,nand zbdenote hydraulic radius, channel width at depthyabove the bed, Manning’s roughness coefficient, and channel bed elevation, respectively.

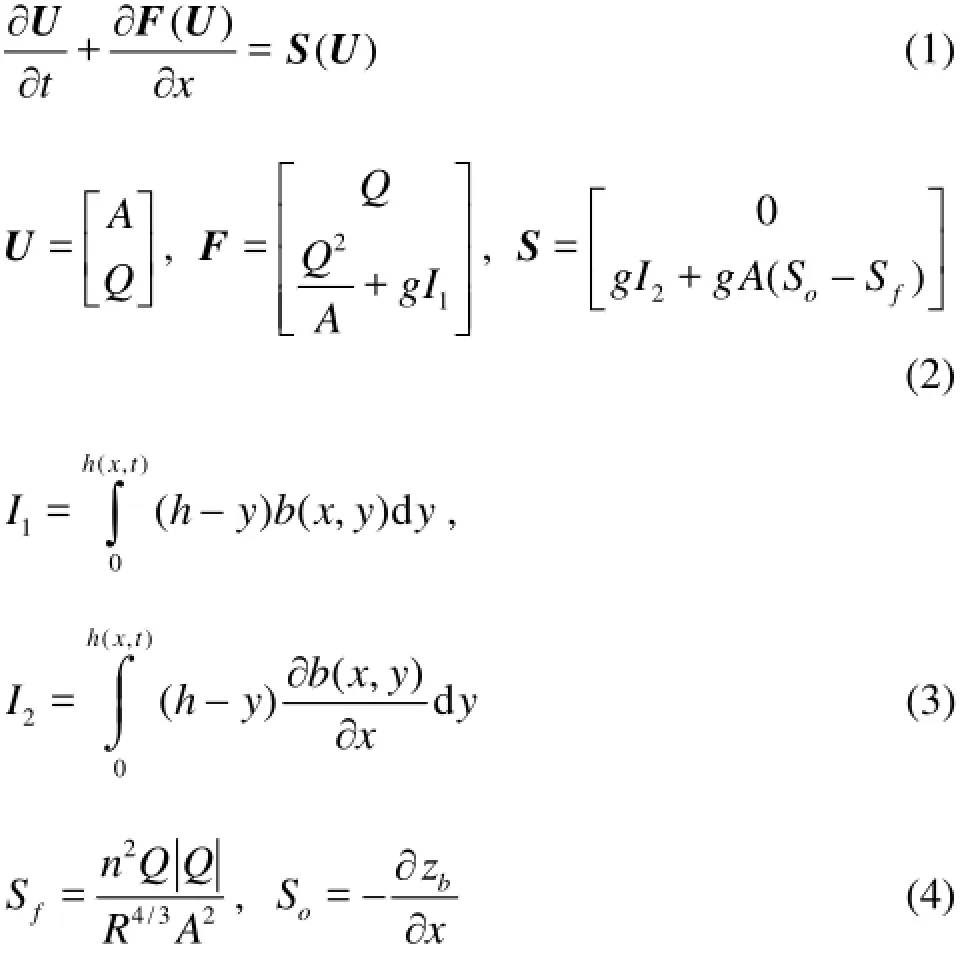
The hydrostatic and wall force terms in Eq.(2) can be simplified using Leibniz integral rule; hence,Eq.(2) can be rewritten as Eq.(5). In this equation,Z is the water surface elevation measured from a datum. This formulation has been successfully implemented in the DG method by Lai and Khan[5].

1.2 Numerical method

In the continuous finite element approach, the field variable U=(A, Q)is forced to be continuous across the boundary, which may cause numerical instability if variation ofUis large across the boundary[18]. The essential idea of the discontinuous finite element method is that the field variable is allowed to be discontinuous across the boundary. Figure 1 illustrates two elements and their boundaries in the DG framework.

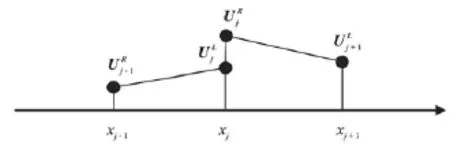
Fig.1 Schematic of discontinuities at element boundaries in the DG framework

In the DG method the domain is discretized such that ?j=[xj,xj+1], where j=1,2,…,Nand Nis the number of elements. First multiplying Eq.(1) with the weight functionv(x)and then integrating over an element,j, results in Eq.(6).

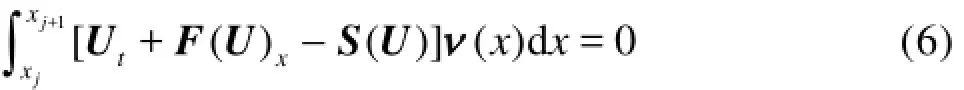
As explicit time stepping schemes are used, each equation is integrated and solved independently. The integral forms of the mass and momentum equations are shown in Eqs.(7) and (8), respectively, where x1and x2are the end coordinates of an element and νi(i=1,2)are linear test or weight functions. In these equations, the flux terms are integrated by parts, where P( x, t)=Qis the flux term for the continuity equation andG( x, t)=Q2/Ais the flux function for the momentum equation. These flux functions at the element boundaries are calculated using approximate Riemann solvers. The approximate variablesA?and Q? as well as any function f?( A, Q)are given by Eq.(9), where νj(j=1,2)are linear shape or interpolating functions. For the Galerkin method, the test and shape functions are the same. To perform the integration, the global coordinates in Eqs.(7) and (8) are transformed to local coordinates.

1.3 Flux treatment

In order to calculate the flux functions (Pand G) at the element boundaries, an approximate HLL Riemann solver is implemented and is given by Eq.(10)[5]. The wave speeds on the left (SL)and right (SR)sides of a boundary are defined using Eqs.(11) and (12), whereu?andc?are defined by Eqs.(13) and (14), respectively, andBis the width of the channel at the water surface.

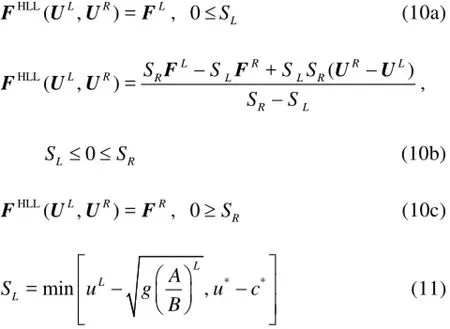
For the dry bed treatment, based on the procedure developed by Ying et al.[19], a small depth (hdry)is prescribed for all the nodes with dry bed. At the end of each time step, if the water depth at any node is less thanhdry, it is reset to hdryand the flow rate at that node is set to zero. The wave speed on the left and right side of the boundary are modified for the partially wet elements based on the formulation of Lai and Khan[5]. Complete details of the application of the DG method to one-dimensional and two-dimensional shallow water flow equations are provided by Lai and Khan[5,20,21].

2. Time integration schemes

For an explicit time marching scheme, Eq.(6) can be rewritten as Eq.(15), where the right hand side is a known vector. Time integration is the last stage in finding a solution. Most of the computational cost can be avoided by the proper choice of time marching scheme. In addition, the choice of a time marching scheme may affect the accuracy of the computed results. Several choices are available to discretize the time derivative term. Three time marching schemes have been evaluated in this study and are described below.

2.1 Forward Euler scheme

The FE scheme is one of the simplest time marching schemes; however, it has only first-order accuracy. Using linear interpolating function, the spatial accuracy is second-order in the DG formulation. Ideally, the time marching scheme should be of the same or higher order. Here, the FE time marching scheme was used to evaluate all possible schemes. The FE formulation is given by Eq.(16), where the time step t+?tis denoted by n +1. Given the solution at timet orn? t(based on the initial conditions or previous time step solution), the solution at t+?tcan be calculated. The FE scheme can be considered as firstorder Runge-Kutta or AB method.

2.2 TVD Runge-Kutta scheme

TVD Runge-Kutta schemes are one of the most widely used multi-stage numerical integration method in the DG framework. The formulation of the second-order TVD Runge-Kutta (RK) numerical integration scheme is shown in Eqs.(17) and (18)[5], where Un,Uint, and Un+1are previous, intermediate and next time steps, respectively. The RK scheme requires an intermediate step to move the solution from time stepnto n+1. This means that all the computations that need to be performed at time stepn, such as evaluation of flux and source terms, must also be performed at the intermediate time step to advance the solution from time stepnto n+1, which increases the computational time. For the RK scheme, the Courant-Friedrichs-Lewy (CFL) condition has to be taken into consideration for stability. The CFL condition is given by Eq.(19), whereP is the order of polynomials for space discretization[5].

2.3 Adam-Bashforth schemes

AB schemes are multi-step explicit numerical integration method. It can be formulated as given by Eq.(20). In this scheme,L(t,U(t))in Eq.(20) is replaced by an interpolation polynomial through the known solution points in time, such asφi(ti,Ui),i= n-k+1,…,n, where n denotes the time level and Uiis the numerical approximation to the exact solution for U (ti)at ti=i?t. Equation (20) can be rewritten as Eq.(21) based on polynomial integration for thek -step AB method.

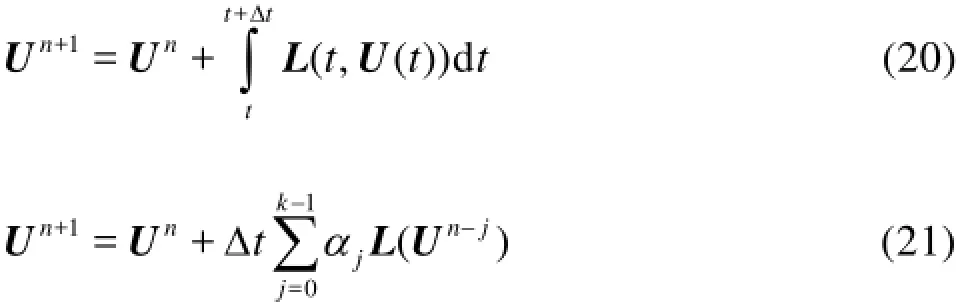
The order of a k -step AB scheme isk . In thisstudy, a 2-step AB scheme (AB-P2) with the coefficients αjfor k=2(given in Table 1) is used. In the AB-P2 scheme, to advance the solution from time step nto n +1, a solution at n-1is required. This means that given the initial conditions(t=0), the AB-P2 scheme cannot be applied and the FE scheme must be used for the very first time step. The first time step involve evaluation of the flux and source terms at t=0. These information (att=0) are saved for use in the AB-P2 scheme for the second time step and beyond. After the first step, the AB-P2 scheme can be applied to advance the solution from time stepnton+1. Therefore, flux and source terms atn-1time step are always available as part of the solution from previous time step, and flux and source terms need to be computed only at time stepnto advance the solution from time stepnto n+1. Thus, multistep methods are advantageous in terms of computational time compared to the multistage methods.

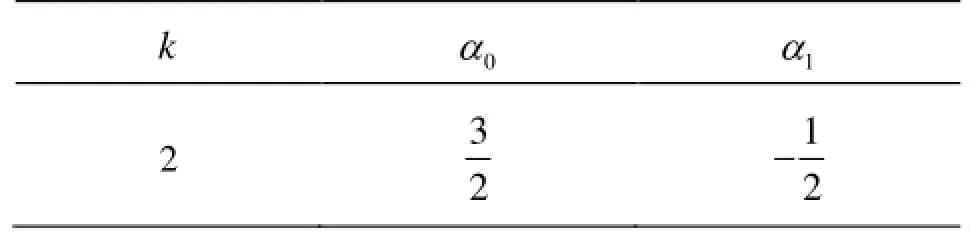
Table1 Coefficients for the second-order Adam-Bashforh scheme

3. Total variation diminishing methods

The TVD property implies that the total variation of the solution will not increase as the solution advances in time. TVD property of a numerical method is given by Eq.(22)[7], where TV is the total variation and is defined by Eq.(23).

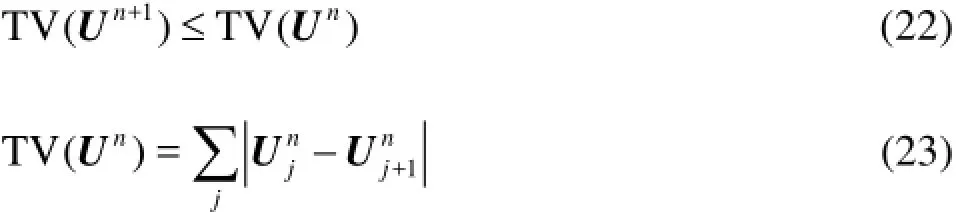
To avoid spurious oscillations in numerical schemes using higher order spatial discretization, gradients near shocks, discontinuities, or sharp changes must be limited. Thus, the use of slope limiters is inevitable. There are many TVD schemes available in the literature for solving convection dominated problems. Use of slope limiters, together with an appropriate high resolution scheme, helps to preserve the TVD property of the numerical model. In addition to applying slope limiters to the discharge, the slope limiters may be applied to water depth, water surface elevation, and flow area. However, it was shown[22]that applying the slope limiter to the water surface produced a well-balanced scheme in rectangular channels with varying bed topography, and for natural channels the flow area based slope limiter was a better choice[5]. Therefore, water surface or flow area based slope limiters is adopted in this study, where applicable.

For an elementl , a general slope limiter formulation for any conserved variable can be written as Eq.(24), where Ul(x)is the average value of a variable over an elementl,xis the midpoint of the element, and σSLdenotes the slope limiting function. Different slope limiters can be developed based on the definition ofσSL. In this paper, three different slope limiters have been used and include minmod, monotonized central (MC), and zero slope limiters. These three slope limiters are given by Eqs.(25)-(27), respectively, where the parameters are defined by Eqs.(28) and (29).

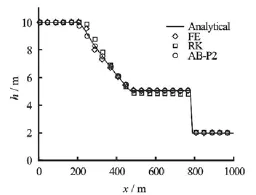
Fig.2 Comparison of the numerical and exact solutions of dam break problem in rectangular channel with different time integration schemes for time step size of 0.4 s

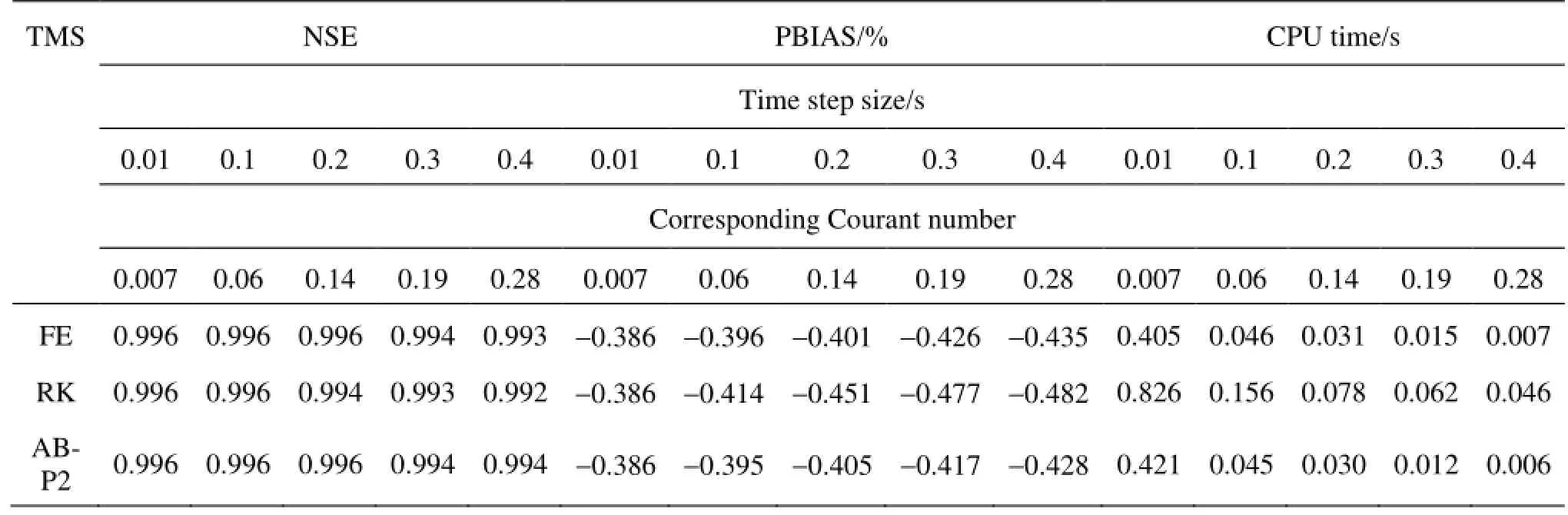
Table2 Accuracy and efficiency analysis in rectangular channel for different time step sizes

Table3 Accuracy and efficiency analysis in trapezoidal channel for different time step sizes

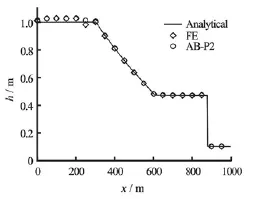
Fig.3 Comparison of the numerical and analytical solutions of dam break problem in trapezoidal channel with different time integration schemes for time step size of 0.2 s

4. Dam break numerical tests with wet bed downstream

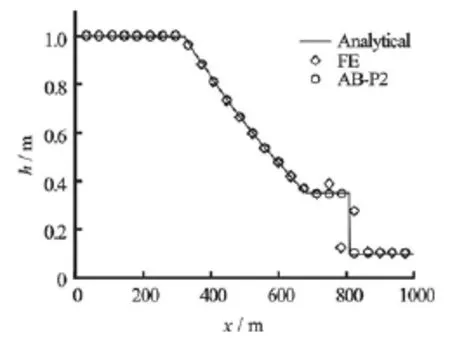
Fig.4 Comparison of the numerical and exact solutions of dam break problem in triangular channel with different time integration schemes for time step size of 0.1 s

Since the ultimate goal of open channel flow simulations is to target long-term natural river modeling, accuracy and efficiency of time integration schemes are extremely important. To evaluate the time stepping schemes, several numerical tests with different cross-section shapes in wet and dry bed conditions were conducted. The numerical tests were performed in rectangular, trapezoidal, triangular, parabolic, and natural channels. The selected shapes provided systematic change from rectangular to natural channel that would help evaluate the time marching schemes. Dam break tests with wet and dry bed conditions downstream of the dam were simulated using different time marching schemes as well as slope limiters. However, to concentrate on the evaluation of time integration schemes initially, only the results of MC slope limiter in wet bed condition are shown. Subsequently, for thedry bed tests, the effects of both slope limiters and time integration schemes are investigated. The behavior of the different slope limiter in case of wet bed is similar to that for the dry bed. Note that, in order to improve the readability of the figures, the amounts of computed data shown is reduced. In tables, TMS and SLT stand for time marching scheme and slope limiter type, respectively.

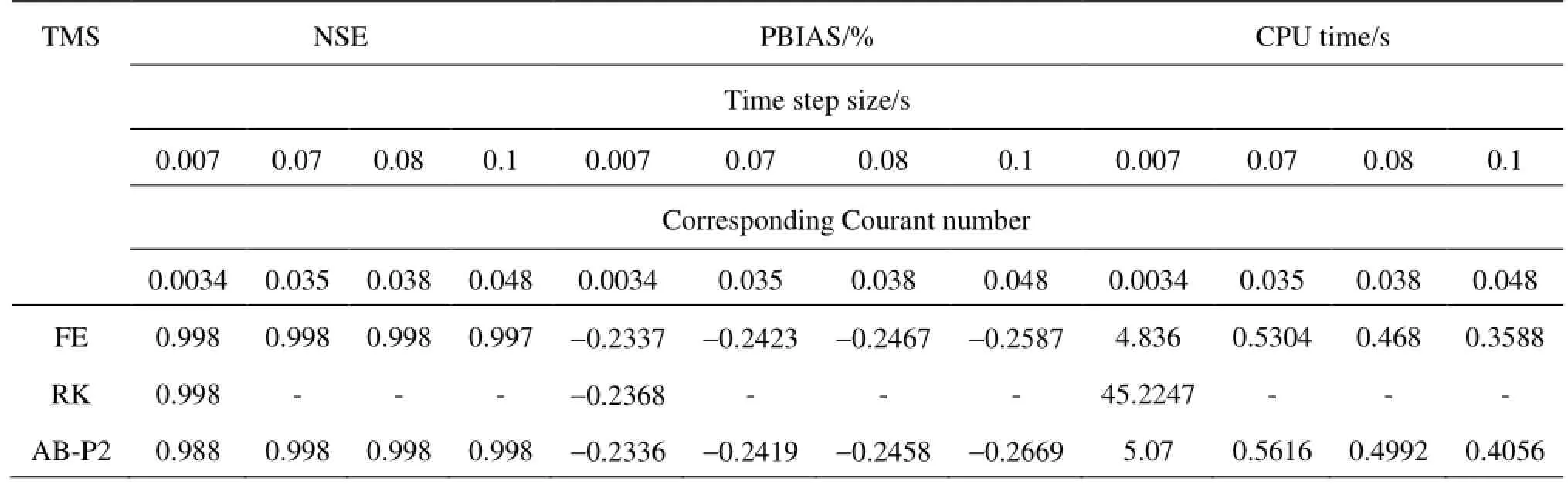
Table4 Accuracy and efficiency analysis in triangular channel with different time step sizes

4.1 Dam break in a rectangular channel with wet bed

Simulation of the idealized dam break problem in rectangular, horizontal channel with wet bed downstream of the dam is a classical test. The channel tested was 1 000 m long with a dam located at 500 m. As an initial condition, the water depths upstream and downstream of the dam were 10 m and 2 m, respectively. The domain was discretized using 100 elements of uniform size. The water surface level at 30 s after the dam removal with time step size of 0.4 s is shown in Fig.2. To evaluate the stability, efficiency, and accuracy, the three different time stepping schemes discussed before were employed with different time step sizes (Courant numbers). Two statistical approaches were used to evaluate the accuracy, and CPU runtime was recorded to compare efficiency of the different time stepping schemes. The results are shown in Table 2.

Based on the tests conducted, RK scheme is the most sensitive to the time step size. It starts to show diffusive behavior for time step size of 0.1 s, while other schemes perform satisfactorily. However, by increasing the time step, the diffusivity of RK scheme remains bounded, but still notable. Up to time step of 0.3 s, the AB-P2 scheme provides the most efficient and accurate results. The FE scheme shows oscillations near the leading edge for time step beyond 0.3 s. In order to have a systematic quantification of accuracy, two statistical approaches based on Moriasi et al.[23], i.e., Nash-Sutcliffe efficiency (NSE) and percent bias (PBIAS), were used, and the results are presented in Table 2. NSE indicates how well the analytical/measured versus simulated data fits the line of unit slope, while PBIAS measures the average positive or negative tendency of the simulated data compared to the observed data. NSE ranges between-∞and 1, with 1 being the optimal value, while PBIAS is an error index with zero being the optimal value and positive/negative values indicate model underestimation/ overestimation bias. Based on the statistical results in Table 2, RK scheme tends to have higher overestimation bias as time step size increases. The CPU runtime for FE and AB-P2 schemes (also shown in Table 2) are very similar. The computational time for the RK scheme (two-stage scheme) is 2-7 times higher (for time step size ranging from 0.01 to 0.4 s and corresponding Courant number of 0.0007 to 0.28) than the other two time marching schemes. For the RK scheme, the extra time was spent in flux and source term calculations as well as slope limiting during the intermediate steps[24]. The largest time step size in Table 2 is the maximum convergeable time step size achievable.

4.2 Dam break in a trapezoidal channel with wet bed

Trapezoidal cross-section is the most common shape in agricultural water distributing systems and therefore selected for this test. A classical dam break problem in horizontal, frictionless, trapezoidal channel was simulated. The channel was 1 000 m long with side slope of 2H:1V and bottom width of 1 m. The dam was located at 500 m with upstream and downstream depths of 1.0 m and 0.1m, respectively. The numerical results are shown at 103.0 s after the dam removal using 400 elements of uniform size. By changing the cross-section shape from rectangular to trapezoidal, the convergence of multistage (RK) scheme is severely impacted especially as the time step size increases. The time steps and the corresponding Courant numbers for different time marching schemes are shown in Table 3. The largest time step for a particular scheme corresponds to the maximum convergeable time step achievable (same for all the following tables that provide time step information). The maxi-mum convergeable time step size for RK scheme is 0.01 s (Courant number of 0.0097), i.e., for time steps greater than 0.01 s, the scheme diverge. For the time step size of 0.2 s, FE scheme shows oscillations near rarefaction wave, while AB-P2 scheme provides accurate results (Fig.3). Considering the PBIAS errors in Table 3, increasing the time step size causes higher error in the FE scheme than the AB-P2 scheme. In other words, the AB-P2 scheme is receding more slowly than the FE scheme from optimum results. The CPU runtimes for all three time marching schemes with different time step sizes are summarized in Table 3. Similar to a rectangular cross section, the RK scheme requires approximately twice the runtime compared to other multistep schemes for the smallest time step size.

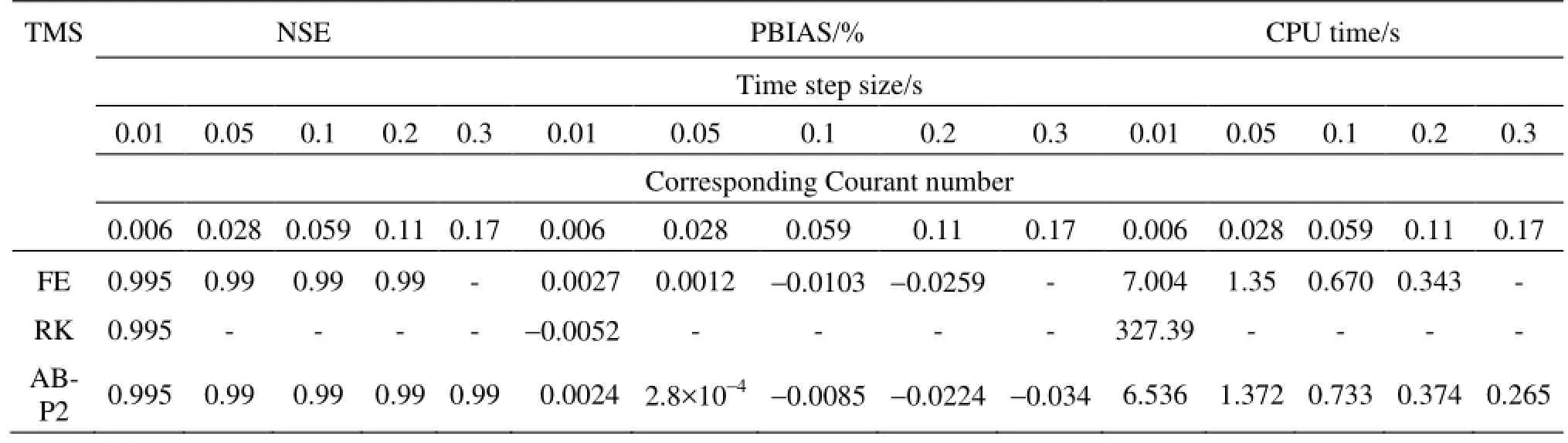
Table5 Accuracy and efficiency analysis in parabolic channel for different time step sizes

4.3 Dam break in a triangular channel with wet bed

In this test, a frictionless, horizontal, triangular channel was considered. The channel was 1 000 m long with side slope of 1H:1V with a dam located at 500 m. The water depths upstream and downstream of the dam were 1 m and 0.1 m, respectively. The domain was discretized using 400 elements of uniform size. The results are shown at 80 s after the dam removal (Fig.4 and Table 4).

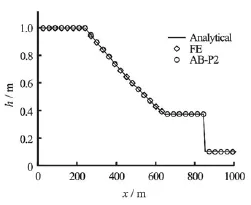
Fig.5 Comparison of the numerical and exact solutions of dam break problem in parabolic channel with different time integration schemes for time step size of 0.3 s

Fig.6 Comparison of numerical and analytical results of the dam break problem with dry bed downstream in rectangular channel using different time marching schemes and slope limiters with maximum convergeable time step size (40.0 s after dam removal)

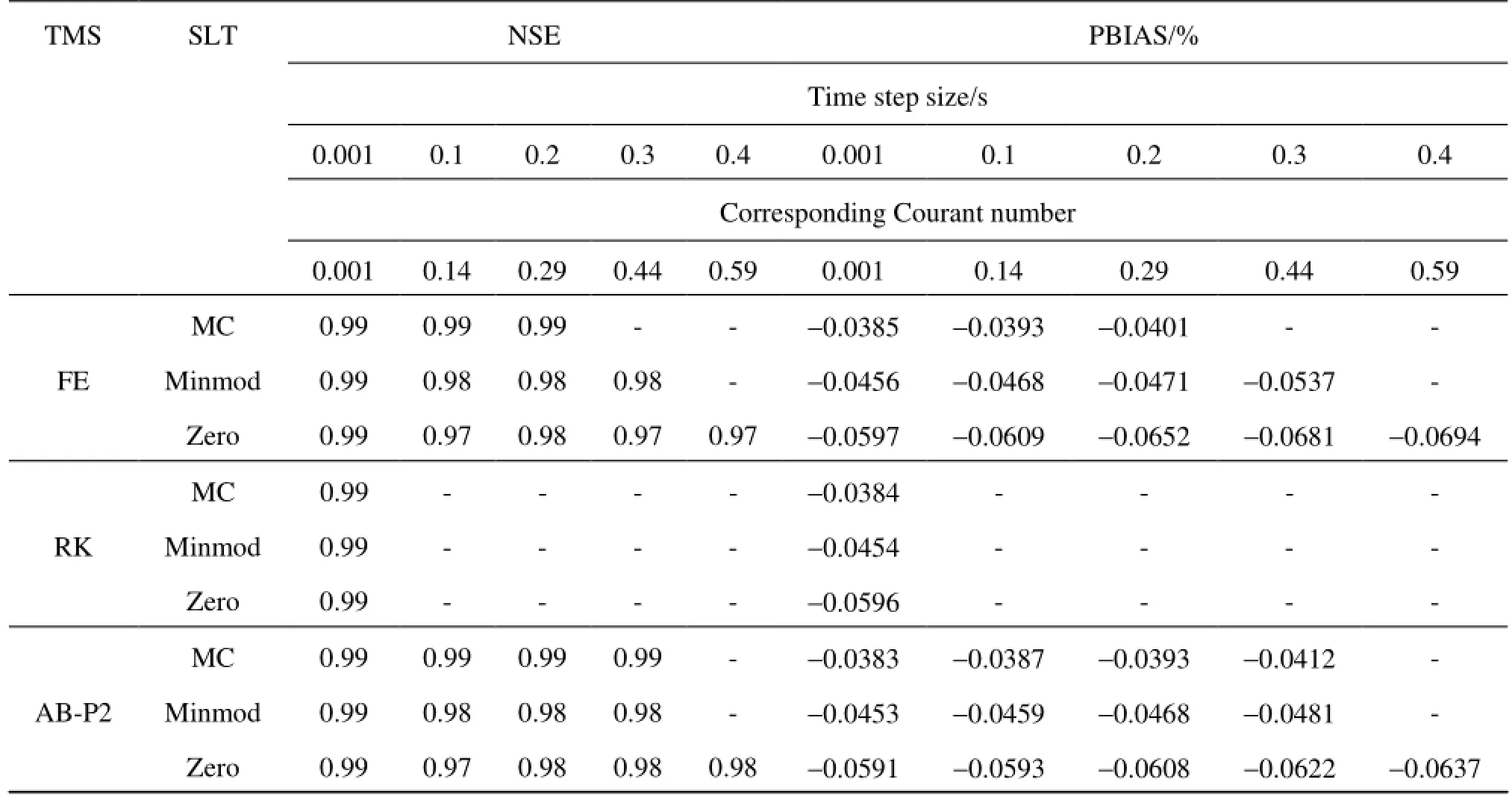
Table6 Accuracy analysis in dry bed rectangular channel for different time step sizes

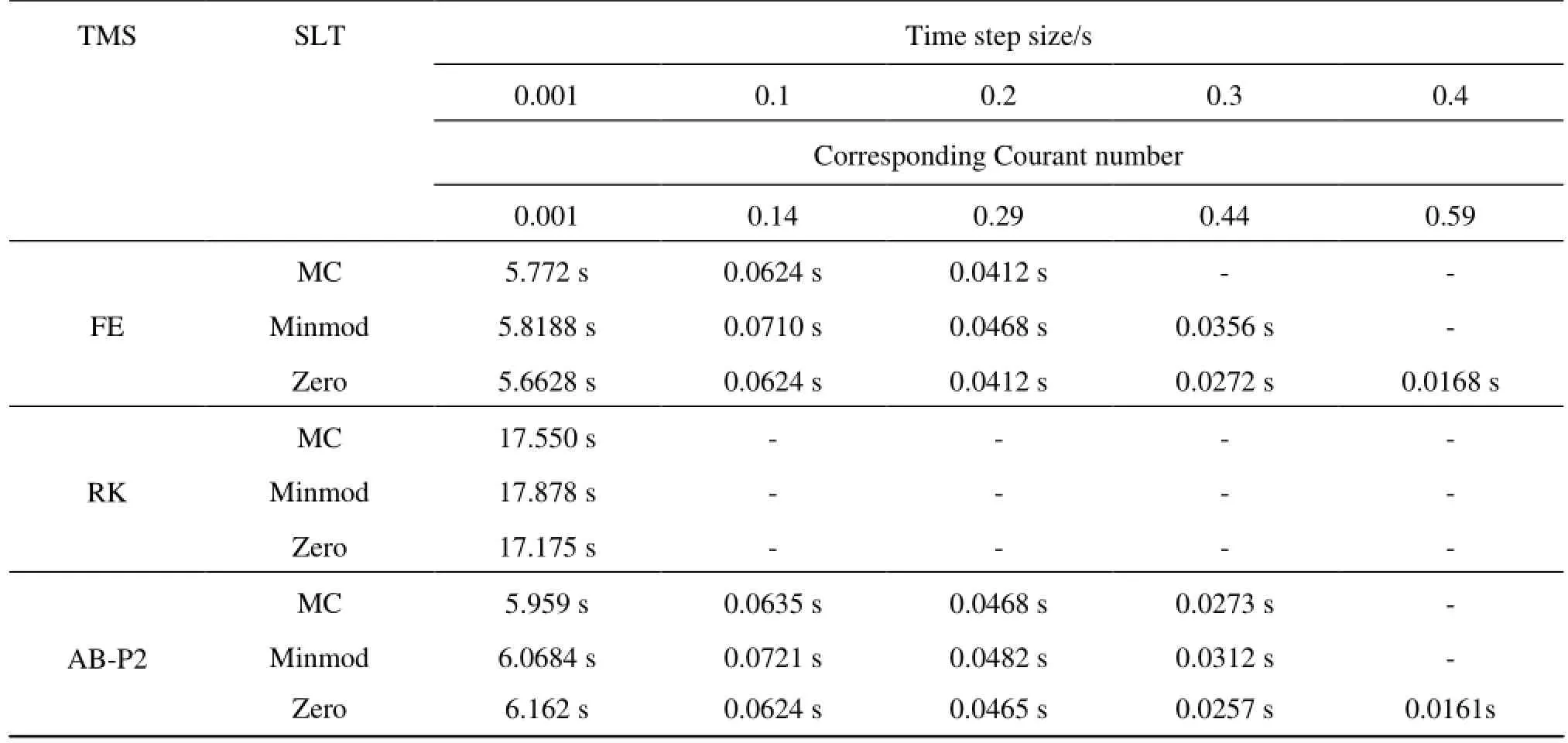
Table7 CPU runtimes in dry bed rectangular channel for maximum time step sizes

Comparisons of the efficiency and accuracy of the tested schemes are presented in Table 4. The RK scheme shows strong dependence on channel cross section shape. For triangular channel, the largest time step size for which the RK scheme shows desirable results is 0.007 s (for the trapezoidal channel the maximum convergeable time step size is 0.01 s), which corresponds to Courant number of 0.0034. The FE and AB-P2 schemes provides convergent results up to 0.1 s (results from FE scheme shows oscillations at the leading edge, see Fig.4). The findings presented in Table 4 indicate that even for small time step size of 0.007 s, the CPU runtime for the RK scheme is 7-fold higher. As before, the runtime for FE and AB-P2 are very similar. However, based on the PBIAS values, for the time step size of 0.1 s (Courant number of 0.048), the numerical results produced by AB-P2 scheme has better accuracy than the FE scheme (Table 4).

To evaluate the impact of spatial discretization on the efficiency and accuracy of different time marching schemes, two more spatial discretizations using200 and 600 elements of uniform sizes were tested. The tests revealed that reducing the element size reduced the maximum convergeable time step size, which is a direct result of CFL condition. Similar to 400 elements test, the FE and AB-P2 schemes had the highest convergeable time step size in these tests. It is obvious that as the element size is reduced, the results will have higher accuracy.

Table8 Accuracy analysis in dry bed trapezoidal channel for different time step sizes

4.4 Dam break in a parabolic channel with wet bed

In this test, a 1 000 m long horizontal, frictionless, parabolic channel with width b=h0.5was modeled. The dam was located at 500 m. The water depths upstream and downstream of the dam were 1.0 m and 0.1 m, respectively. The domain was discretized using 400 elements of uniform size and the numerical results are shown at 100 s after dam removal (Table 5 and Fig.5). The maximum possible time step size for this test is 0.3 s (Courant number of 0.17) for the AB-P2 scheme as presented in Fig.5. The reported NSE and PBIAS statistical values indicate that the RK scheme is biased towards underestimation. The maximum convergeable time step size for the RK scheme is 0.01 s (Courant number of 0.006), while the other two time marching schemes are able to produce reasonable results with larger time step sizes. Only the AB-P2 scheme provides optimal results for time step size of 0.3 s with a PBIAS value of -0.034%, while the other time marching schemes fully (RK) or partially (FE) diverge at this time step size. Table 5 lists the CPU runtimes for the parabolic channel test case. It is observed that adapting more complex geometries tremendously affect the CPU runtime of RK scheme, the required CPU time for RK is 45 times higher than the other multistep schemes for the time step size of 0.01 s. The change in spatial discretization has same effects as discussed for the triangular channel.

5. Dam break numerical tests with dry bed downstream

In these tests, the behavior of the time marching schemes and slope limiters in simulating unsteady flows over dry beds is evaluated. The critical point in obtaining an optimal numerical result in cases of dry bed is the proper selection of hdryand time step size. Here, two tests in rectangular and trapezoidal channels with dry bed downstream of the dam are presented with three different slope limiters. The numerical results in triangular and parabolic channels with dry bed downstream of the dam have similar characteristics and are not presented here.

5.1 Dam break in rectangular channel with dry bed

The geometry and length of the rectangular channel considered in this test were the same as for the wet bed test. The depth upstream of the dam was 1m and the downstream channel was dry (assigned a value of hdry). For simulation hdryof 7×10-4m was used. The domain was discretized using 100 elements of uniform size and the results are shown at 40 s after the dam removal. Ideally, the best scheme (for a given hdry) is the one that not only utilizes largest possible time step size (lowest CPU runtime), but also shows the best accuracy. Generally, ashdryis lowered, the time step size must be reduced.

The results for the maximum convergeable time step sizes for different slope limiters are shown inFig.6. The figure clearly shows that the zero slope limiter is over diffusive. For the three slope limiters tested, the time step size of 0.001 s (Courant number of 0.001) is the limit for RK method to achieve convergeable results. The maximum usable time step size for FE and AB-P2 is 0.4 s (Courant number of 0.59) for zero slope limiter (Table 6). The accuracy analysis shows that the numerical results obtained have higher overestimation bias using zero slope limiter followed by minmod and MC (Table 6). Although zero slope limiter allows for the largest time step size, it does so at the expense of accuracy as it is over diffusive. For a given time step size and time stepping scheme, the MC slope limiter provides the most accurate solution, followed by minmod and zero slope limiters, respectively. Thus, choice of a slope limiter and time stepping scheme can be based on efficiency and accuracy requirements.

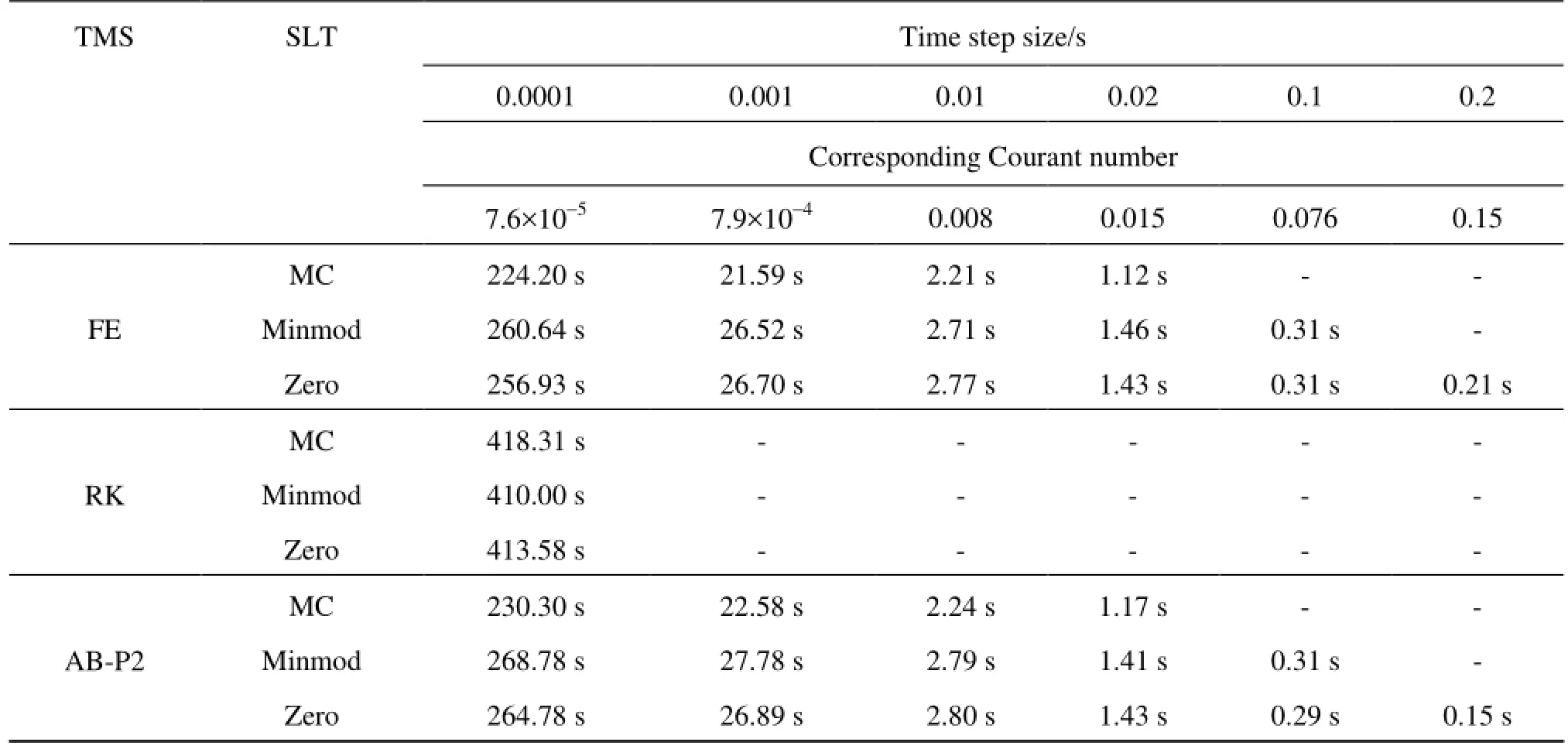
Table9 CPU runtimes in dry bed trapezoidal channel for maximum time step sizes

Comparison of CPU runtimes for all time marching schemes with different slope limiters is presented in Table 7. As evident, RK scheme requires runtimes about three times that of other multistep schemes for the same time step size. It should be noted that the use of different slope limiters does not affect the CPU runtime appreciably.

5.2 Dam break in trapezoidal channel with dry bed

To confirm the numerical findings in rectangular channel, the procedure was repeated in trapezoidal channel with the channel properties as discussed earlier for the wet bed test. Similar to the previous test, hdrywas set to 7×10-4m for dry cell simulations. Table 8 shows the NSE and PBIAS values for different time steps for the time marching and slope limiter schemes being evaluated. In accordance with previous results, RK scheme has the least maximum possible time step size. Based on CPU runtimes presented in Table 9, AB-P2 is the most efficient scheme. The accuracy and efficiency of time marching schemes can be compared with respect to slope limiter types. For larger time steps, MC slope limiter provides most accurate results followed by minmod. Largest convergeable time step size can be applied using zero slope limiter both in FE and AB-P2 schemes, however, the accuracy obtained using MC and minmod is higher.

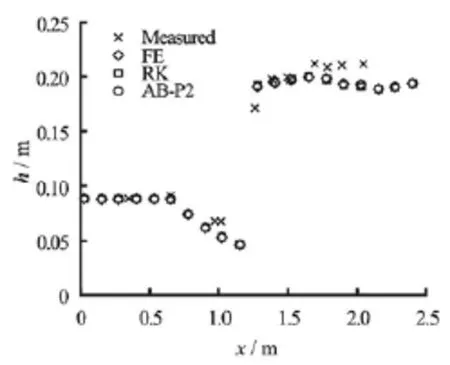
Fig.7 Simulation of hydraulic jump in divergent channel using MC slope limiter with time step size of 0.002 s

6. Hydraulic jump in a divergent channel-steady state test case

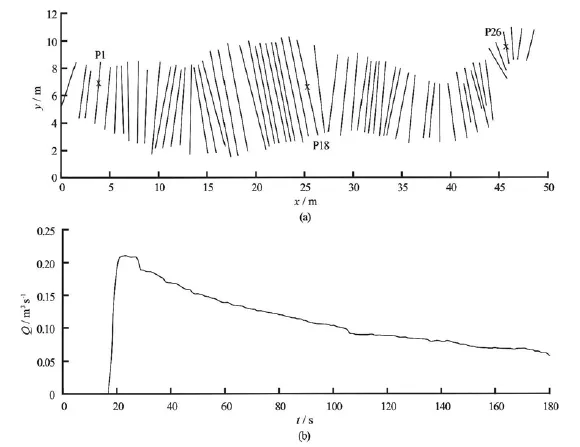
Fig.8 Positions of Toce River cross sections (a), inflow discharge hydrograph (b)

Different time marching schemes are further studied in a steady state case for accuracy and efficiency. In this test, a hydraulic jump was simulated in a divergent channel. Khalifa[25]performed physical model test in a 2.5 m long horizontal channel with a rectangular cross section. The channel width is given by Eq.(30). The inlet discharge was set to 0.0263 m3/s and the upstream and downstream depths were set at 0.088 m and 0.195 m, respectively. As an initial condition, water surface level was linearly interpolated between the upstream and downstream depths and the inlet discharge was specified at all nodes. Thus, the flow condition was supercritical at the inlet and subcritical at the outlet. The domain was discretized using 100 elements of uniform size. The test was simulated using different time step sizes with MC slope limiter. Numerical results for the time step size of 0.002 s are shown in Fig.7. Maximum convergeable time step size for RK scheme is 0.002 s, while other schemes provide results up to time step size of 0.008 s. The required CPU runtime for RK time marching scheme is about twice that of other schemes for the time step size of 0.002 s. All schemes converged to the same steady state solution.

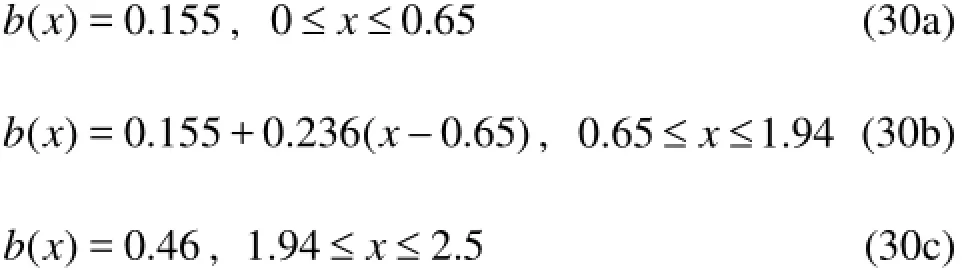
7. Case study-Toce River dam break

To evaluate the performance of the time marching schemes in natural rivers, the Toce River dam break test using MC slope limiter was simulated. A physical model (1:100 scale) of 5 km reach of the Toce valley located in the northern part of Italy was constructed[26]to study the flood following the dam break in the Toce River. Selected gauges (P1, P18, and P26) along the main river axis were used for comparing the simulated results with the measured data. These gauges and the inflow discharge at the upstream section are presented in Fig.8. The lines in Fig.8 represent river cross sections at which topographic information are available. The simulated hydrographs, using different time marching schemes, at the gauge locations are compared with the measure data. In this simulation, 62 cross-sections with non-uniform mesh, ranging from element size of 0.25 m to 1.94 m, were utilized. The maximum convergeable time step sizes for different time marching schemes are presented in Table 10. These time step sizes were chosen to obtain the best possible solutions as shown in Fig.9. The dry bed criterion,hdry, was selected as 7×10-6m and the Manning roughness coefficient was 0.02 s/m1/3[26].

Figure 9 compares simulated and measured hydrographs for the three time marching schemes. All time marching schemes provides similar results for the maximum convergeable time step sizes. Based on the time step size and CPU runtime, presented in Table 10, it is obvious that the AB-P2 scheme is the most efficient followed by FE and RK schemes. This test clea-rly shows that in non-prismatic natural channels small increases in time step can lead to huge time saving. Considering the test conditions (non-prismatic and non-uniform mesh) AB-P2 is the most efficient scheme.

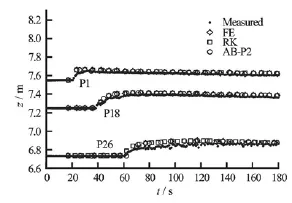
Fig.9 Comparison of numerical and measured results in Toce River with different time marching schemes and slope limiters for maximum convergeable time step size

Table1 0 Maximum possible time step size for Toce River test

8. Conclusions

The performance of the forward Euler (FE), second-order TVD Runge-Kutta (RK), and second-order Adam-Bashforth (AB-P2) time integration schemes along with monotonized central, minmod, and zero slope limiters has been investigated in the discontinuous Galerkin finite element method for shallow water flow equations in wet and dry bed conditions. The AB-P2 scheme is more efficient than the other two schemes considered in this study, while maintaining the second-order accuracy. For the same time step size, the multistep method (AB-P2) is two to three times more efficient than multistage method (RK). For the tests conducted in this study, AB-P2 consistently provides the largest convergeable time step size, thus providing efficiency that can be much higher than the RK scheme, which provides the lowest convergeable time step size. The results clearly demonstrate that for long term real world shallow water flow simulations, the RK scheme is less efficient than the AB-P2 and FE schemes; however AB-P2 provides higher accuracy than the FE scheme as it is secondorder accurate.

For the dry bed tests, the RK scheme requires either higher dry bed criterion or lower time step size, a higher dry bed criterion may lead to mass conservation problems and inaccurate results. The FE scheme has better performance in terms of efficiency than the RK scheme and has similar accuracy for similar time step sizes. The RK scheme requires the application of a slope limiter and flux and source terms computations at the intermediate time step. As slope limiters are inherently diffusive in nature, the second order accuracy of the RK scheme is compromised due to the application of slope limiter at the intermediate step. This results in the FE and RK schemes having similar accuracy. The MC slope limiter had the best accuracy; however it is limited by the time step size. Considering NSE and PBIAS statistical parameters, zero slope limiter is the most diffusive scheme and numerical results obtained by zero slope limiter are overestimated but it can allow larger time step size.

The channel cross section geometry has a major influence on the time step size. The required time step and the Courant number decrease successively for rectangular, trapezoidal, parabolic, and triangular channel cross section geometry for the three time marching schemes considered in this paper. The intermediate time step in the RK scheme is the main cause for lower efficiency, accuracy, and Courant number requirement. Hence, it is advisable to use AB-P2 time marching scheme with MC slope limiter for best accuracy and efficiency.

[1] COZZOLINO L., MORTE R. D. and GIUDICE G. D. et al. A well-balanced spectral volume scheme with the wetting-drying property for the shallow-water equations[J]. Journal of Hydroinformatics, 2012, 14(3): 745-760.

[2] DüBEN P. D., KORN P. and AIZINGER V. A discontinuous/continuous low order finite element shallow water model on the sphere[J]. Journal of Computational Physics, 2012, 231(6): 2396-2413.

[3] PETACCIA G., NATALE L. and SAVI F. et al. Flood wave propagation in steep mountain rivers[J]. Journal of Hydroinformatics, 2013, 15(1): 120-137.

[4] ESCOBAR-VARGAS J. A., DIAMESSIS P. J. and GIRALDO F. X. High-order discontinuous elementbased schemes for the inviscid shallow water equations: Spectral multidomain penalty and discontinuous Galerkin methods[J]. Applied Mathematics and Computation, 2012, 218(9): 4825-4848.

[5] LAI W., KHAN A. A. Discontinuous Galerkin method for 1D shallow water flow in nonrectangular and nonprismatic channels[J]. Journal of Hydraulic Engineering, ASCE, 2012, 138(3): 285-296.

[6] LAI Wencong, KHAN Abdul A. Modeling dam-break flood over natural rivers using discontinuous Galerkin method[J]. Journal of Hydrodynamics, 2012, 24(4): 467-478.

[7] KHAN A. A., LAI W. Modeling shallow water flows using the discontinuous Galerkin method[M]. Boca Raton, USA: CRC Press, 2014.

[8] LAI W., KHAN A. A. Discontinuous Galerkin method for 1D shallow water flows in natural rivers[J]. Engineering Applications of Computational Fluid Mechanics, 2012, 6(1): 74-86.

[9] LI B. Q. Discontinuous finite elements in fluid dynamics and heat transfer[M]. London, UK: Springer, 2006.

[10] BOKHOVE O. Flooding and drying in discontinuous Galerkin finite-element discretizations of shallow-water equations. Part 1: One dimension[J]. Journal of Scientific Computing, 2005, 22(1): 47-82.

[11] HUBBARD M. E., GARCIA-NAVARRO P. Flux difference splitting and the balancing of source terms and flux gradients[J]. Journal of Computational Physics, 2000, 165(1): 89-125.

[12] BERMUDEZ A., VáZQUEZ M. E. Upwind methods for hyperbolic conservation laws with source terms[J]. Computers and Fluids, 1994, 23(8): 1049-1071.

[13] YING X., KHAN A. A. and WANG S. S. Y. An upwind method for one-dimensional dam break flows[C]. Proceedings of XXX IAHR Congress. Thessaloniki, Greece, 2003.

[14] BURBEAU, A., SAGAUT P. and BRUNEAU Ch.-H. A problem-independent limiter for high-order Runge-Kutta discontinuous Galerkin methods[J]. Journal of Computational Physics, 2001, 169(1): 111-150.

[15] HASSANZADEH H., ABEDI J. and POOLADI-DARVISH M. A comparative study of flux-limiting methods for numerical simulation of gas–solid reactions with Arrhenius type reaction kinetics[J]. Computers and Chemical Engineering, 2009, 33(1): 133-143.

[16] DIXIT J. Comprehensive programming in C and numerical analysis[M]. New Delhi, India: Laxmi Publications, 2006.

[17] QIU J., KHOO B. C. and SHU C. A numerical study for the performance of the Runge-Kutta discontinuous Galerkin method based on different numerical fluxes[J]. Journal of Computational Physics, 2006, 212(2): 540-565.

[18] ZHOU J. G., CAUSON D. M. and MINGHAM C. G. et al. The surface gradient method for the treatment of source terms in the shallow-water equations[J]. Journal of Computational Physics, 2001, 168(1): 1-25.

[19] YING X., KHAN A. A. and WANG S. S. Y. Upwind conservative scheme for the Saint Venant equations[J]. Journal of Hydraulic Engineering, ASCE, 2004, 130(10): 977-987.

[20] LAI W., KHAN A. A. A discontinuous Galerkin method for two-dimensional shock wave modeling[J]. Modelling and Simulation in Engineering, 2011, 2011: 782832.

[21] LAI W., KHAN A. A. A discontinuous Galerkin method for two-dimensional shallow water flows[J]. International Journal for Numerical Methods in Fluids, 2012, 70(8): 939-960.

[22] LAI W., KHAN A. A. Discontinuous Galerkin method for 1-D shallow water flow with water surface slope limiter[J]. International Journal of Civil and Environmental Engineering, 2011, 3(3): 167-176.

[23] MORIASI D., ARNOLD J. and Van LIEW M. et al. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations[J]. Transactions of the ASABE, 2007, 50(3): 885-900.

[24] LAI Wencong, KHAN Abdul A. Time stepping in discontinuous Galerkin method[J]. Journal of Hydrodyamics, 2013, 25(3): 321-329.

[25] KHALIFA A. M. Theoretical and experimental study of the radial hydraulic jump[D]. Doctoral Thesis, Windsor, Canada: University of Windsor, 2000.

[26] FRAZAO S. S., TESTA G. The Toce River test case: Numerical results analysis[C]. Proceedings of the 3rd CADAM Workshop. Milan, Italy, 1999.

* Biography: SAFARZADEH MALEKI Farzam (1983-), Male, Ph. D., Assistant Professor

KHAN Abdul A.,

E-mail: abdkhan@clemson.edu