On a Discrete Fractional Boundary Value Problem with Nonlocal Fractional Boundary Conditions

HUANG Zhong-min,XIE Zuo-shi,HOU Cheng-min

(1.Department of Mathematics,Yanbian University,Yanji 133002,China;2.The School of Economics and International Trade,Zhejiang University of Finance and Economics,Hangzhou 310018,China)

On a Discrete Fractional Boundary Value Problem with Nonlocal Fractional Boundary Conditions

HUANG Zhong-min1,XIE Zuo-shi2,HOU Cheng-min1

(1.Department of Mathematics,Yanbian University,Yanji 133002,China;2.The School of Economics and International Trade,Zhejiang University of Finance and Economics,Hangzhou 310018,China)

In this paper,we investigate the nonlinear fractional dif f erence equation with nonlocal fractional boundary conditions.We derive the Green’s function for this problem and show that it satisf i es certain properties.Some existence results are obtained by means of nonlinear alternative of Leray-Schauder type theorem and Krasnosel-skii’s f i xed point theorem.

discrete fractional calculus;green’s function;nonlocal fractional boundary conditions;existence of solution;f i xed point

§1.Introduction

In this paper,we consider a discrete fractional boundary value problem(FBVP)

subject to the boundary conditions

where f(t+ν?1,·,·):[ν?1,ν+b]Nν-1×R×R?→[0,+∞)is a continuous function and g∈C([ν?2,ν+b+1]Nν-2,[0,+∞)),ξ∈[0,b]N0,ν∈(1,2],α,a∈[0,1],with ν,α,a∈R,satisfy both ν?α?1≥0 and a(ν+ξ?α)ν?α?1≤(ν?α?1)(ν+b?α)ν?α?2.Fractional calculus is an emerging fi eld recently drawing attention from both theoretical and applied disciplines. During he last two decades it has been successfully applied to problems in computational biology,medical sciences,economics,physics and several fi elds in engineering[1-8].In 1989, a pioneering work has been done by Miller and Ross[9].In particular,Atici and Eloe[10]have already analyzed the conjugate discrete FBVP with delta derivative.Somewhat earlier Atici and Eloe[11]considered a discrete fractional IVP.On the other hand,the present author considered in[12]a discrete fractional right-focal BVP,whereas in[13]he considered continuity properties of discrete fractional IVP.Other recent work has concerned discrete FBVPs with a variety of boundary conditions as well as discrete fractional variational problems and modeling-see[14-20]. A recent paper by C S Goodrich[18]discussed a discrete FBVPs with nonlocal conditions(i.e.,△νy(t)=f(t+ν?1,y(t+ν?1))subject to y(ν?2)=g(y),y(ν+b)=0 with 1＜ν≤2).Because these problems have been extensively studied in the classical case,it seems mathematically interesting to investigate these sort of problem in the fractional case.Motivated by the above discussions,the main aim of this paper is to study the existence of solutions for the FBVP (1)～(3).

The plan of this paper is as follows.In section 2,we recall some useful preliminaries. In section 3,we give the corresponding Green’s function and some properties of the Green’s function.Finally,by the properties of the Green’s function and f i xed point theorem on cones, some sufficient conditions for the existence of at least one positive solutions for the FBVP are established.

§2.Preliminaries

We f i rst collect some basic lemmas for manipulating discrete fractional operators.These and other related results can be found in the references[10,14].

First,for any integer β,we let Nβ={β,β+1,β+2,···}.We def i ne,for any t and α for which the right-hand side is de fi ned.We also appeal to the convention that if t+1?α is a pole of the Gamma function and t+1 is not a pole,then tα=0.

Def i nition 1.1The αth fractional sum of f for α＞0 is def i ned by△?αaf(t)=(s),for t∈Na+α.We also def i ne the αth fractional dif f erence for α＞0 by△αf(t):=△MΔα?Mf(t)where t∈Na+αand M∈N is chosen so that 0≤M?1＜α≤M.

Lemma 1Let t and ν be any numbers for which tνand tν?1are de fi ned.Then△tν= νtν?1.Moreover,tνis increasing in t whenever ν∈(0,1)and decreasing whenever ν∈(?1,0).

Lemma 2Let 0≤M?1＜ν≤M.Then△?ν△νy(t)=y(t)+C1tν?1+C2tν?2+···+for some Ci∈R,with 1≤i≤M.

Lemma 3For β＞0 and allμ∈? for which the following is def i ned,we f i nd that

Lemma 4Let B be a Banach space and let K?B be a cone.Assume that ?1and?2are open sets contained in B such that 0∈?1and ?1??2.Assume,further,that T: K∩(?2?1)?→K is a completely continuous operator.If either

1.||Ty||≤||y||for y∈K∩??1and||Ty||≥||y||for y∈K∩??2

or

2.||Ty||≥||y||fory∈K∩??1and||Ty||≤||y||for y∈K∩??2.

Then T has at least one fi xed point in K∩(?2?1).

Lemma 5Let B be a Banach space with C?B closed and convex.Assume that U is a relatively open subset of C with 0∈U and T:U?→C is completely continuous.Then either

1.T has a fi xed point inU

or

2.There exist u∈?U and γ∈(0,1)with u=γTu.

§3.Derivation of a Green’s Function

For convenience,we introduce the following notations.

Theorem 2.1Let h:[ν?1,ν+b]Nν-1?→R and g:Rb+4?→R be given.The unique solution of the FBVP

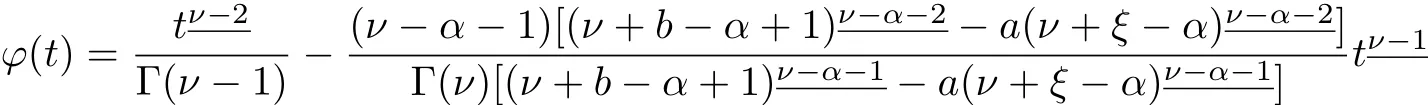
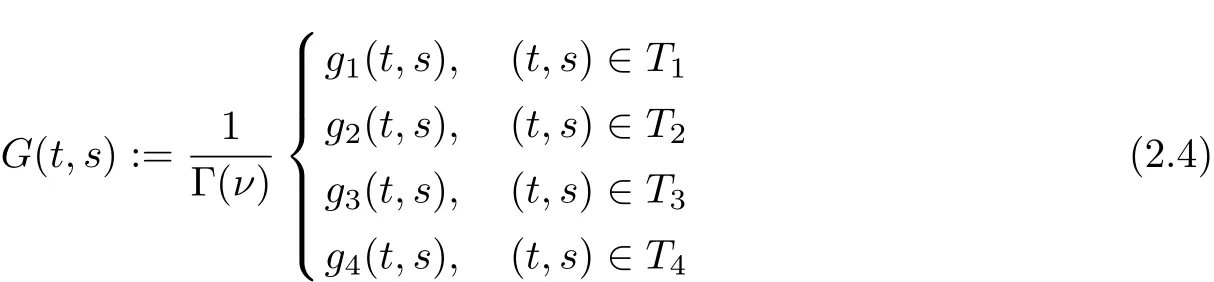
andis the Green’s function for the problem.

ProofUsing Lemma 2,we get that y(t)=?△?νh(t+ν?1)+[ν?2,ν+b+1]Nν-2.By boundary condition(2.2),we have y(ν?2)=C2Γ(ν?1)=g(y),On the other hand,by applying boundary condition(2.3)and△αy(t)=

Consequently,we can deduce that y(t)has the form

Theorem 2.2The function ?(t)is given in Theorem 2.1 satisf i es 0＜?(t)≤1 when

ProofFor any t∈[ν?2,ν+b+1]Nν-2,since

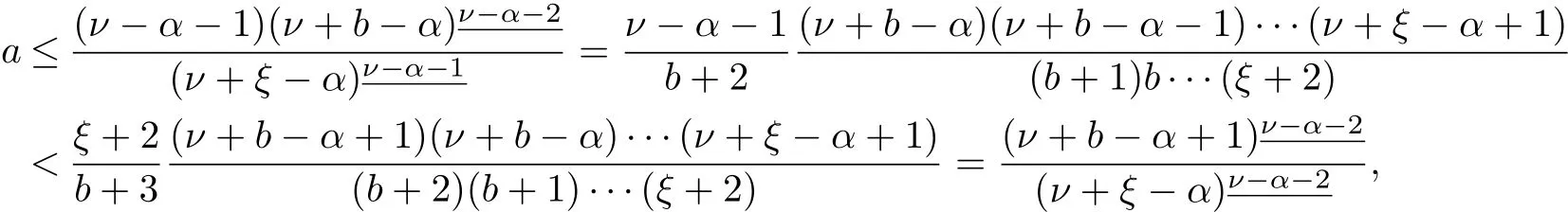
then it follows that

and

1.G(t,s)≤G(s+ν?1,s).

2.There exists positive functions γ(s)and β(s)such that

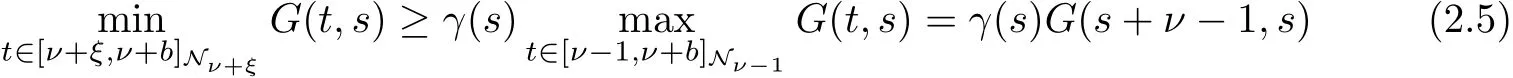
and

Therefore,we have that g2(t,s)is decreasing with respect to t on[s+ν?1,b+ν]Ns+ν-1.Similarly, we can verify that g1(t,s)is also decreasing with respect to t on[s+ν?1,b+ν]Ns+ν-1.

We can conclude from above that G(t,s)is increasing with respect to t on[ν?1,s+ν?1]Nν-1and G(t,s)is decreasing with respect to t on[s+ν?1,b+ν]Ns+ν-1.Hence G(t,s)≤G(s+ν?1,s). On the other hand,we know that

where λ(s)=min{g2(t,s),g4(t,s)}.Let

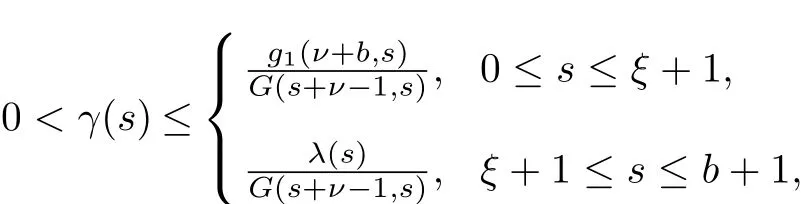
where

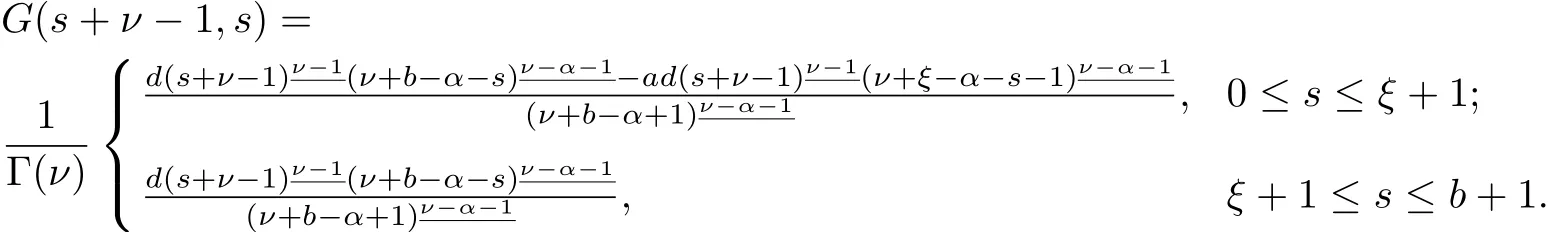
Hence,(2.5)has been verif i ed.By Lemma 1,we have Then,(2.6)has been verif i ed.

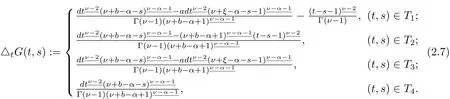
where G is the Green’s function from Theorem 2.1.This observation is of principal importance in what follows.

Corollary 2.1Let y be a f i xed point of operator T.If g is nonnegative,then there exist a constant~γ∈(0,1),such that

ProofObserve Lemma 6,we f i nd that there exist constants γ,β∈(0,1)such that

and

From Theorem 2.2,we know that there is a real number 0＜γ0＜1 such thatmin ?(t)=?(ν+b)=γ0and henc

Now we denote~γ by

since

evidently,~γ∈(0,1),moreover,we can deduce that

and

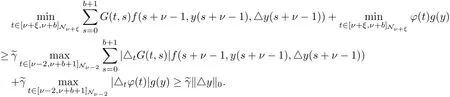
Hence,mint∈[ν+ξ,ν+b]Nν+ξy(t)≥~γ(‖y‖0+‖△y‖0)≥~γ‖y‖.Then the proof is completed.

§4.Existence of Positive Solutions

Denote by K the cone on Banach space B,

where~γ is def i ned by(2.10).

We will use the known properties of G(t,s)to obtain the necessary estimates of‖Ty‖so that Lemma 4 may be invoked.Moreover,we need not then deduce a separate Green’s function for each possible manifestation of g(y).

Lemma 7Let T be the operator def i ned as(2.9)and K as(3.1).Assume in addition that both f and g are nonnegative.Then T:K?→K. ProofNote that

and

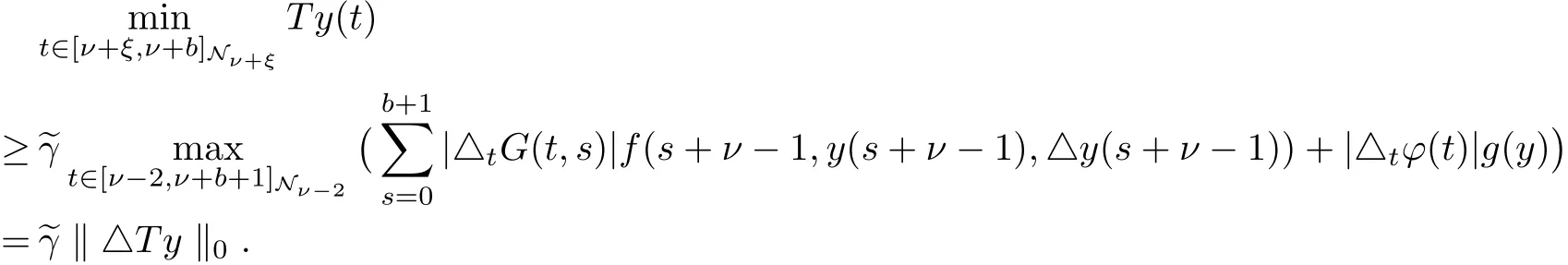
Now,for convenience in what follows,let

Now,we introduce some conditions that will helpful in the sequel,these conditions place some control on the growth of the nonlinearity f(t,y,△y),as well as the functional g(y)appearing in(1)～(3).

(H1)There exist a number r＞0 such that f(t,y,△y)≤r whenever 0≤y≤r;

(H2)There exist a number r＞0 such that f(t,y,△y)≥λr whenever~γr≤y≤r;

(G1)There exist a number r＞0 such that g(y)≤η?r whenever 0≤‖y‖≤r.

Theorem 4.1Suppose that there exist two distinct number r1and r2,with r1,r2＞0, such that conditions(H1),(H2)and(G1)hold at r1and conditions(H2)hold at r2.Furthermore, assume that each of f and g is nonnegative.Then problem(1)～(3)has a positive solution, whose norm lies between r1and r2.

ProofLet T be the operator de fi ned as(2.9).Note that T is a summation operator on discrete fi nite set,hence,T is trivially completely continuous and T:K?→K.Without loss of generality,suppose that 0＜r1＜r2,put ?1={y∈C([ν?2,ν+b+1]Nν-2,R):‖y‖＜r1}.

Then we have that for y∈K∩??,

and

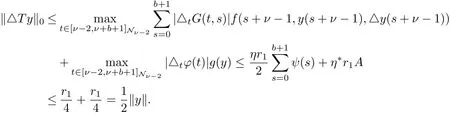
Thus‖Ty‖≥max{‖Ty‖0,‖△Ty‖0}≥‖y‖,i.e.,‖Ty‖≥‖y‖for y∈K∩??2.

Applying by Lemma 4,we can deduce that T has a f i xed point y0∈K,this function y0(t)is a positive solution to problem(1)～(3),and y0satisf i es r1＜‖y‖＜r2.The proof is completed.

Theorem 4.2Assume that f:[ν?1,ν+b]Nν-1×R×R?→[0,+∞)satisf i es the follow conditions

1.f(t,y,△y)is continuous with respect to y and△y on R2.

2.There exist three real-valued functions n,m,l∈C[ν?1,ν+b]Nν-1such that f(t+ν?1,y(t+ν?1),△y(t+ν?1))≤n(t+ν?1)+m(t+ν?1)y(t+ν?1)+l(t+ν?1)△y(t+ν?1) for all t∈[ν?1,ν+b]Nν-1and y∈R,△y∈R.Ifwhere Z(t+ν?1){|m(t+ν?1)|,|l(t+ν?1)|}.Then the FBVP(1)～(3)has at least one positive solution.

ProofLet U={y∈K,‖y‖＜ε,‖g(y)‖＜ω},where

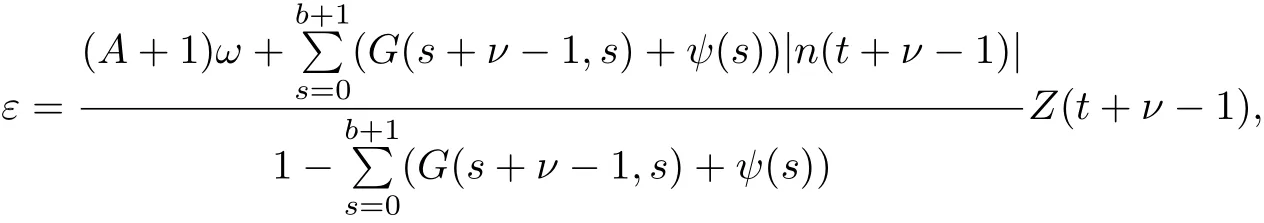
A be denoted in Theorem 2.And T:1),△y(s+ν?1))+?(t)g(y).Firstly,T is obviously completely continuous.Then assume that there exist y∈K and δ∈(0,1)such that y=δTy,we claim that‖y‖/=ε.In fact,we have that

and

Therefore,we get that Applying by Lemma 5 we get that y∈/?U,then T has a fi xed point y∈U.Hence,FBVP (1)～(3)has at least a positive solution.

We now provide another result that yields the existence of at least one positive solution.In what follows,we shall assume that f(t,y,△y)has the special form f(t,y,△y)≡F1(t)F2(y,△y). To facilitate this result,we introduce the following additional conditions on F2and g.

Theorem 4.3Suppose that conditions(H3),(H4)and(G2)hold.Moreover,assume that each of F1,F2and g is nonnegative.The problem(1)～(3)has at least one positive solution.

ProofBy(H3),we know that there is a number α1＞0 sufficiently small such that F2(y,△y)≤η′1y and F2(y,△y)≤η′2△y hold for all 0＜y≤α1and 0＜△y≤α1.

And where we choose η1and η2sufficiently small so that which η1=max{η′1,η′2}and

Similarly,condition(G2)implies that we may f i nd a number α2＞0 such that

holds whenever 0＜‖y‖≤α2and where η2is chosen so that

Now,pu∩tα?=min{α1,α2}and set ?3={y∈K,‖y‖＜α?},then it follows that for all y∈??3K,inequalities(3.4)～(3.8)implies that

and

On the other hand,condition(H4)implies that there exists a number α3＞0 such that F2(y,△y)≥‖y‖0,F2(y,△y)≥‖△y‖0hold for all y,△y＞α3.Let η3=min{},

whenever y≥α3.Furthermore,we can choose η3sufficiently large such that

Observe that by putting

we f i nd that for‖y‖=α??,

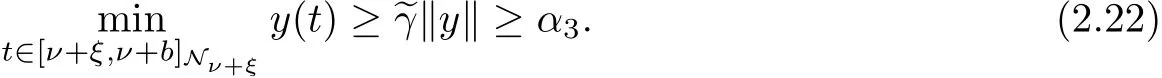
Now,set ?4={y∈K,‖y‖＜α??},recall that 0＜?(t)≤1 for each t∈[ν?2∩,ν+b+1]Nν-2, from which follows that ?(t)g(y)≥0,then we can fi nd that for y∈??4K.Inequalities (3.9)～(3.10),(3.12)and equality(3.11)imply that Tyν,s)F1(s+ν?1)≥‖y‖,hence‖Ty‖≥max{‖Ty‖0,‖△Ty‖0}≥‖y‖whenever y∈??4K.

Consequently,we can deduce that T has a fi xed point in the set K∩??.But this mean43that(1)～(3)has a positive solution.And this completes the proof.

NoteIn this paper,we have shown by way of an explicit Green’s function that(1)～((3) continuously generalizes the conjugate FBVP considered in[10]and provided some analysis of Green’s function.As an application of our analysis,we also have shown that under standard assumptions on nonlinearity f(y1,y2,y3),problem(1)～(3)may admit a positive solution.The conclusions in this paper generalize and extended certain of the results presented in[10,12,18]. It might be interesting to generalize certain of the results here to delta-nabla problems as well as by allowing f to depend upon one or two of the fractional di ff erence△py,△qy.

[1]BASSUKAS I D.Comparative Gompertzian analysis of alterations of tumor growth patterns[J].Cancer Res, 1994,54:4385-4392.

[2]BASSUKAS I D,MAURER Schultze B.The recursion formula of the Gompertz function:A simple method for the estimation and comparison of tumor growth curves[J].Growth Dev Aging,1988,52:113-122.

[3]COUSSOT C,KALYANAM S,YAPP R,et al.Fractional derivative models for ultrasonic characterization of polymer and breast tissue viscoelasticity[J].IEEE Trans Ultrason Ferroeletrc Freq Control Apr,2009, 56(4):715-726.

[4]JUMARIE G.Stock exchange fractional dynamics def i ned as fractional exponential growth driven by(usual) Gaussian white noise:Application to frac-tional Black-Scholes equations[J].Insurance Math Econom,2008, 42:271-287.

[5]MAGIN R L.Fractional calculus in bioengineering[J].Crit Rev Biomed Eng,2004,32(1):1-104.

[6]MARONSKI R.Optimal strategy in chemotheraphy for a Gompertzian model of cancer growth[J].Acta Bioeng Biomech,2008,10(2):81-84.

[7]NORTON L A.Gompertzian model of human breast cancer growth[J].Cancer Res,1988,48:7067-7071.

[8]SABATIER J,AGRAWAL O P,TENREIRO Machado J A.Advances in Fractional Calculus:Theoretical Developments and Applications in Physics and Engineering[M].Springer:Springer-Verlag New York Inc, 2007:7.

[9]MILLER K S,ROSS B.Fractional Dif f erence Calculus,Proceedings of the International Symposium on Univalent Functions,Fractional Calculus and Their Applications[D].Koriyama,Japan:Nihon University, 1988:139-152.

[10]ATICI F M,ELOE P W.Two-point boundary value problems for f i nite fractional dif f erence equations[J].J Dif f erence Equ Appl,2011,17(4):445-456.

[11]ATICI F M,ELOE P W.Initial value problems in discrete fractional calculus[J].Proc Amer Math Soc, 2009,137(3):981-989.

[12]COODRICH C S.Solutions to a discrete right-focal fractional boundary value problem[J].Int J Dif f erence Equ,2010,5(2):195-216.

[13]GOODRICH C S.Continuity of solutions to discrete fractional initial value problems[J].Comput Math Appl,2010,59(11):3489-3499.

[14]FERHAN M,ATICI,SEVGI Seng¨ul.Modeling with fractional dif f erence equations[J].J Math Anal Appl, 2010,369(1):1-9.

[15]BASTOS N R O,RUI A C Ferreira,DELFIM F M Torres.Necessary optimality conditions for fractional dif f erence problems of the calculus of variations[J].Discrete Contin Dyn Syst,2011,29(2):417-437.

[16]GOODRICH C S.On a discrete fractional three-point boundary value problem[J].J Dif f erence Equ Appl, 2012,18(3):397-415.

[17]GOODRICH C S.Some new existence results for fractional dif f erence equations[J].Int J Dyn Syst Dif f er Equ,2011,3(1):145-162.

[18]GOODRICH C S.Existence and uniqueness of solutions to a fractional dif f erence equation with nonlocal conditions[J].Comput Math Appl,2011,61(2):191-202.

[19]GOODRICH C S.Existence of a positive solution to a system of discrete fractional boundary value problems[J].Appl Math Comput,2011,217(9):4740-4753.

[20]GOODRICH C S.On positive solutions to nonlocal fractional and integer-order dif f erence equations[J].Appl Anal Discrete Math,2011,5(1):122-132.

[21]ATICI F M,ELOE P W.A transform method in discrete fractional calculus[J].Int J Dif f erence Equ,2007, 2(2):165-176.

tion:39A12,44A25,26A33

1002–0462(2014)04–0539–14

date:2013–02–19

Supported by the National Natural Science Foundation of China(11161049)

Biography:HOU Cheng-min(1963-),female,native of Yanji,Jilin,a professor of Yanbian University,M.S.D., engages in discrete dynamical system.

CLC number:O175.8Document code:A