Diffusion of chemically reactive species in Casson fluid flow over an unsteady permeable stretching surface*

MUKHOPADHYAY Swati

Department of Mathematics, The University of Burdwan, Burdwan-713104, W. B., India, E-mail: swati_bumath@yahoo.co.in

VAJRAVELU Kuppalapalle

Department of Mathematics, Department of Mechanical, Materials and Aerospace Engineering, University of Central Florida, Orlando, Florida 32816 - 1364, USA

Diffusion of chemically reactive species in Casson fluid flow over an unsteady permeable stretching surface*

MUKHOPADHYAY Swati

Department of Mathematics, The University of Burdwan, Burdwan-713104, W. B., India, E-mail: swati_bumath@yahoo.co.in

VAJRAVELU Kuppalapalle

Department of Mathematics, Department of Mechanical, Materials and Aerospace Engineering, University of Central Florida, Orlando, Florida 32816 - 1364, USA

(Received May 30, 2012, Revised October 22, 2012)

In this paper we investigate the two-dimensional flow of a non-Newtonian fluid over an unsteady stretching permeable surface. The Casson fluid model is used to characterize the non-Newtonian fluid behavior. First-order constructive/destructive chemical reaction is considered. With the help of a shooting method, numerical solutions for a class of nonlinear coupled differential equations subject to appropriate boundary conditions are obtained. For the steady flow, the exact solution is obtained. The flow features and the mass transfer characteristics for different values of the governing parameters are analyzed and discussed in detail.

chemical reaction, Casson fluid, mass transfer, unsteady stretching, suction/injection

Introduction

Processes involving the effects of mass transfer have attracted the attention of researchers due to applications in chemical processing equipments[1]. The driving force for mass transfer is the difference in concentration. There are some fluids which react chemically with some ingredients present in them.

In the recent years, the boundary-layer flows of non-Newtonian fluids have been given considerable attention due to ever increasing engineering applications. In order to obtain a thorough cognition of non-Newtonian fluids and their various applications, it is necessary to study their flow behaviors. It is well known that the mechanics of non-Newtonian fluids present a special challenge to engineers, physicists and mathematicians. The non-linearity can manifest itself in a variety of ways in many fields, such as food processing, drilling operations and bio-engineering. The Navier-Stokes theory is inadequate for such fluids and no single constitutive equation is available in the literature which exhibits the properties of all fluids. Because of the complexity of these fluids, there is not a single constitutive equation which exhibits all properties of such non-Newtonian fluids. Thus a number of non-Newtonian fluid models have been proposed. In literature, the majority of non-Newtonian fluid models are concerned with simple models like the power-law and grade two or grade three fluids[2,3]. These simple fluid models have shortcomings that render to results not having accordance with fluid flows in the reality. The power-law model has a vast usage in modeling fluids with shear-dependent viscosity but it cannot predict the effects of elasticity. The fluids of grade two or grade three can account for the effects of elasticity but the viscosity in these models is not shear-dependent, and also they cannot predict the effects of stress relaxation. A subclass of rate type fluids namely the Maxwell model can predict the stress relaxation. This rheological model, also, excludes the complicating effects of shear-dependent viscosity from any boundary-layer analysis. There is another fluid model for non-Newtonian fluid, namely the Casson fluid, examples of which include jelly, tomato sauce, honey, soup, concentrated fruit juices, etc.. Human blood canalso be treated as a kind of Casson fluid. Due to the presence of several substances like, protein, fibrinogen and globulin in aqueous base plasma, human red blood cells can form a chainlike structure, known as aggregates or rouleaux. If the rouleaux behaves like a plastic solid then there exists a yield stress that can be identified with the constant yield stress in the Casson fluid. The Casson fluid can be defined as a shear thinning liquid which is assumed to have an infinite viscosity at zero rates of shear, a yield stress below which no flow occurs and a zero viscosity at an infinite rate of shear. Boyd et al.[4]investigated the Casson fluid flow for the steady and oscillatory blood flows.

In most of the above studies, the flow, temperature, and the concentration fields are considered to be at steady state. However, in practice, the flow, heat, and mass transfer fields are unsteady: This could be due to a sudden stretching of the flat sheet or due to a step change in the temperature of the sheet. When the stretching velocity and the concentration (surface temperature) of the sheet vary with time, not much research is being done. Some authors[5-7]studied the problem for unsteady isothermal stretching surface by using a similarity method to transform governing time-dependent boundary layer equations into a set of ordinary differential equations. Sharidan et al.[8]studied the unsteady flow and heat transfer over a stretching sheet in a viscous and incompressible fluid. Recently, Mukhopadhyay[9,10],Chamkha et al.[11]obtained similarity solutions for unsteady flow and heat transfer over a stretching sheet under different conditions. Bhattacharyya et al.[12]analyzed the effects of slip on unsteady boundary-layer stagnation point flow past a stretching sheet. Of late, Hayat et al.[13]discussed the three-dimensional flow of Jeffery fluid past a stretching surface.

The process of suction and injection (blowing) is also important in many engineering applications such as in the design of thrust bearing and radial diffusers, and thermal oil recovery. Suction is applied to chemical processes to remove reactants. Blowing is used to add reactants, to cool the surfaces, to prevent corrosion or scaling and to reduce the drag. Injection or withdrawal of fluid through a porous heated or cooled bounding wall is of practical interest in problems involving film cooling, control of boundary-layers, and so forth.

Despite the overwhelming applications and frequent occurrence of non-Newtonian behavior in industry and technology, not much attention has been paid so far to analyze the Casson fluid flow and mass transfer past an unsteady stretching surface. Motivated by this, an attempt is made in this paper to extend the work of Andersson et al.[5]for Casson fluid flow and mass transfer. With the help of similarity transformation the governing partial differential equations are transformed into the ordinary differential equations, and the reduced ordinary differential equations are then solved numerically using a shooting method. Exact solution of the momentum equation for the steady case is also obtained. The effects of unsteadiness parameter, the Casson parameter, the suction/injection parameter, the Schmidt number and the reaction rate parameter on the velocity and the concentration fields are investigated and analyzed with the help of their graphical representations.

1. Equations of motion

Consider two-dimensional laminar boundarylayer flow and mass transfer of an incompressible Casson fluid over an unsteady stretching sheet. The fluid flow and mass transfer start at =0t. The sheet emerges out of a slit at the origin (=0x, =0y) and moves with the velocity U(x,t)=bx/(1-αt) where b＞0, α≥0 are constants with b the initial stretching rate.

The rheological equation of state for an isotropic and incompressible flow of a Casson fluid is

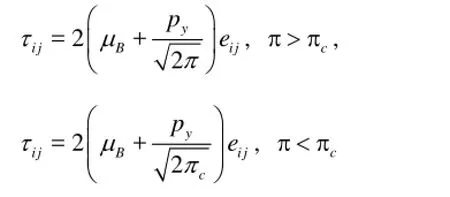
Here π=eijeijand eijis the (i,j)thcomponent of the deformation rate, π is the product of the component of deformation rate with itself,cπ is a critical value of this product based on the non-Newtonian model,Bμ is plastic dynamic viscosity of the non-Newtonian fluid, andyp is the yield stress of the fluid. LetwC be the concentration at the sheet and C∞is the concentration far away from the sheet. Also, let there be a firstorder homogeneous chemical reaction of species with reaction rate constant1k.

Under these assumptions, the continuity, momentum[14]and concentration equations are, in the usual notations,

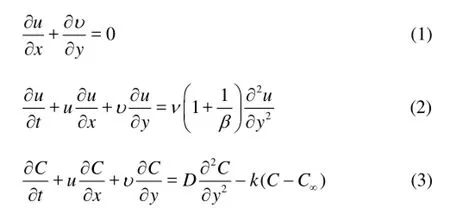
where u and υ are the velocity components in the x and y directions, ν is the kinematic viscosity of the fluid,is parameter of the Casson fluid, C is the concentration, D is the diffusion coefficient of the diffusing species in the fluid, k(t)=k0/ (1)tα- is the time-dependent reaction rate, 0k＞stands for destructive reaction whereas 0k＜ stands for constructive reaction, and0k is a constant.

1.1 Boundary conditions

The appropriate boundary conditions for the problem are

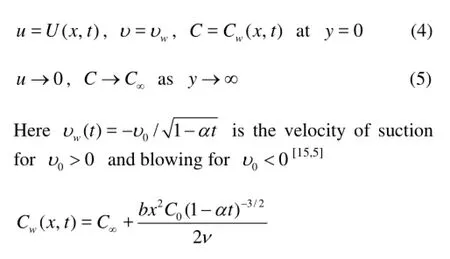
where0C is a (positive or negative) reference concentration at x=0. The expressions for U(x,t),Cw(x,t), k(t),υw(t) are valid for time t＜α-1.

1.2 Method of solution

By introducing u=?ψ/?y, υ=-?ψ/?x and φ=(C-C∞)/(Cw-C∞) (ψ being stream function) and defining

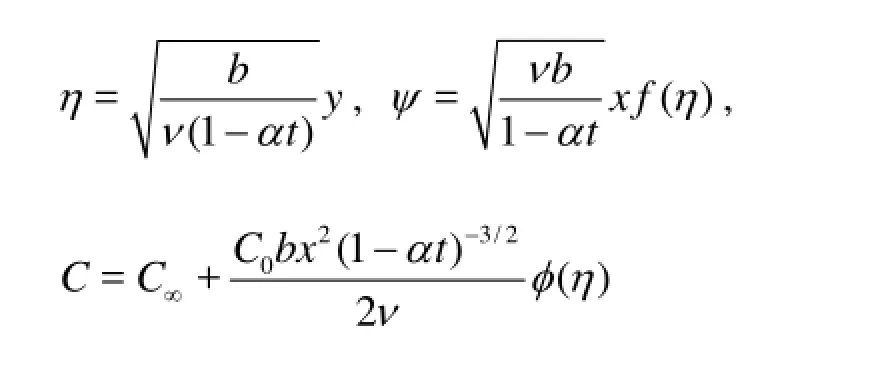
the governing equations can be reduced to

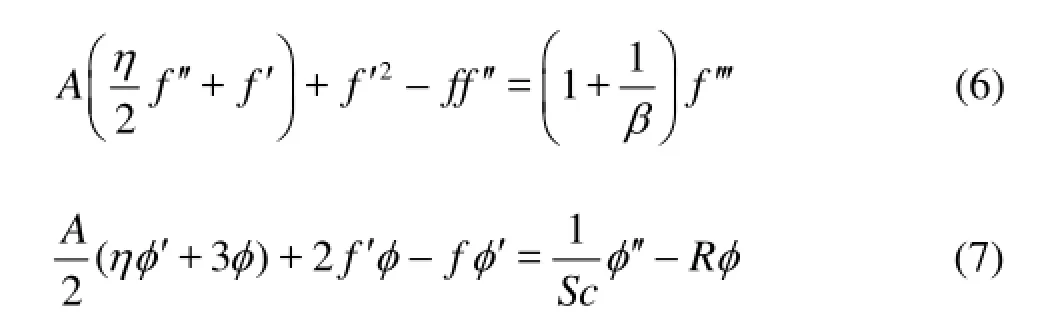
where =/Abα is the unsteadiness parameter, =Sc ν/D is the Schmidt number, and R=k0/b is the reaction rate parameter.

The boundary conditions (4) and (5) then become

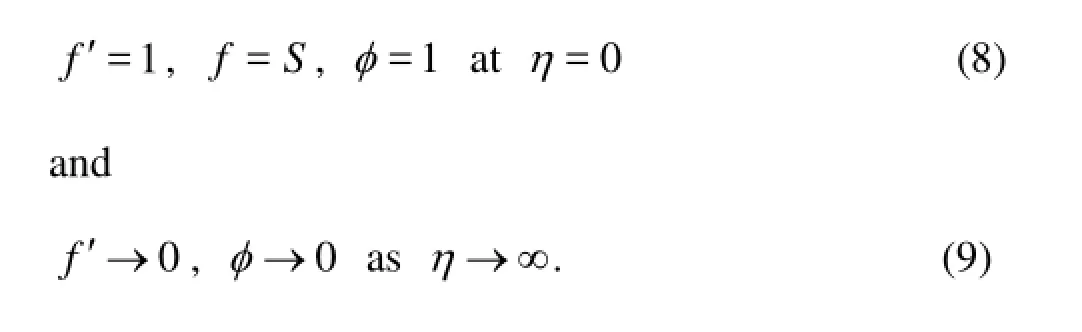
2. Exact solution for a special case

The exact solution of Eq.(6) subject to the corresponding boundary conditions for steady case, i.e., when =A0, is given by

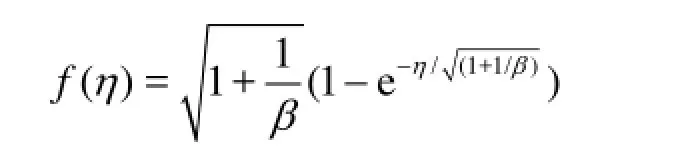
3. Method of numerical solutions

The differential Eqs.(6) and (7) along with boundary conditions (8)-(9) are solved by converting to an initial value problem. We set

In order to integrate Eqs.(10) and (11) as an initial value problem we require a value for (0)p. That is, we need (0)f′ and (0)φ′, but no such values are given. The most important factor of shooting method is to choose the appropriate finite values of η∞. In order to determine η∞for the boundary value problem, we start with some initial guess values for a particular set of physical parameters to obtain (0)f′ and (0)φ′. The solution processes will be repeated with another appropriate value of η∞until two successive values of f′(0) and φ′(0) differ only by the specified significant digit. The last value of η∞is finally chosen to be the most appropriate value of the limit η∞for that particular set of parameters. The value of η∞may changefor another set of physical parameters[16]. Once the finite value of η∞is determined, the integration is carried out. We compare the calculated values for f′and φ at =η10 say with the given boundary conditions f′(10)=0 and φ(10)=0, and then adjust the estima- ted values of (0)f′ and (0)φ′ to give a better appro- ximation for the solution. We take the series of values for (0)f′ and (0)φ′, and apply the fourth-order cla- ssical Runge-Kutta method with the step-size =h0.01. The above procedure is repeated until we get the resu- lts up to the desired degree of accuracy 10–5.

4. Results and discussion

In order to validate the numerical method used in this study, a comparison is made with available results of Sharidan et al.[8]and Chamkha et al.[11], corresponding to the skin-friction coefficient (0)f′ for the unsteady flow of viscous incompressible fluid (see Table 1), and found a very good agreement.

Table 1 The values of (0)f′ for various values of unsteadiness parameter A for Newtonian fluid

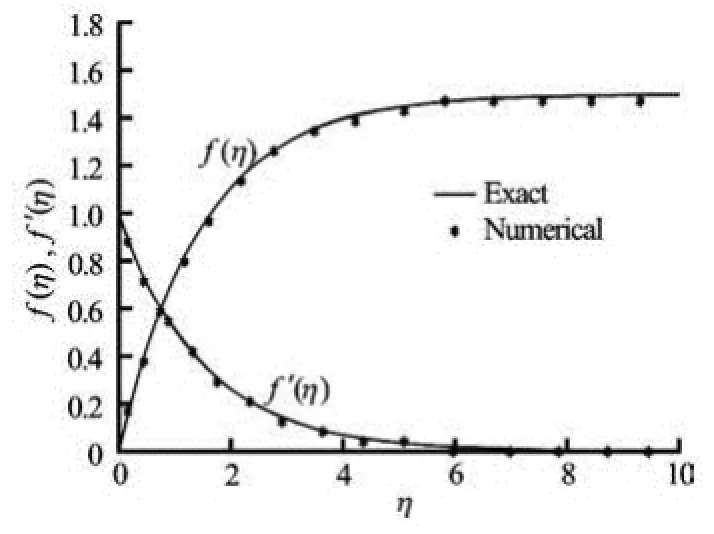
Fig.1 Stream function ()fη and velocity ()fη′ with η for steady motion

Moreover, to verify the accuracy of the present numerical scheme, a comparison of the results corresponding to the stream function profiles ()fη and velocity profiles ()fη′ with the exact solution for steady motion (=0)A is presented in Fig.1, and found an excellent agreement. Furthermore, to analyze the behavior of the velocity and concentration fields for Casson fluid, a comprehensive numerical computation is carried out for various values of the parameters, and the results are presented in Figs.2-7.

Fig.2(a) Velocity profiles for variable unsteadiness parameter A in the presence of suction

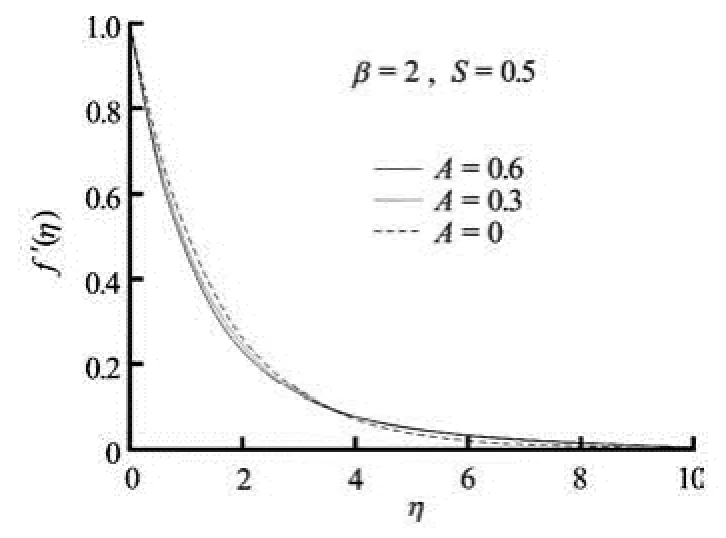
Fig.2(b) Velocity profiles for variable unsteadiness parameter A in the presence of blowing

Fig.2(c) Concentration profiles for variable unsteadiness parameter A in presence of suction/blowing

Figure 2(a) exhibits the velocity profiles for several values of the unsteadiness parameter A in the presence of suction. It is seen that the velocity along the sheet decreases initially with the increase in the unsteadiness parameter A. That is, there is a reduction in the thickness of the momentum boundary layer near the wall, but away from the wall, the fluid velocity increases with increasing unsteadiness. Similar behaviour of velocity field is also noted in case of blowing (Fig.2(b)).

Figure 2(c) represents the effects of the unsteadiness parameter on the concentration distribution in thepresence of suction/injection. From this figure, it is noticed that the concentration at a point is found to decrease significantly with increasing unsteadiness parameter. However, the rate of mass transfer decreases with increasing A. As the unsteadiness parameter A increases, less solute is transferred from the sheet to the fluid, hence, the concentration ()φη decreases (Fig.2(c)). Since the fluid flow is caused solely by the stretching sheet, and the sheet surface concentration is higher than free stream concentration, the velocity and concentration decrease with increasing η. It is important to note that the rate of mass transfer is much faster for higher values of the unsteadiness parameter, whereas it may take longer time for steady flow.

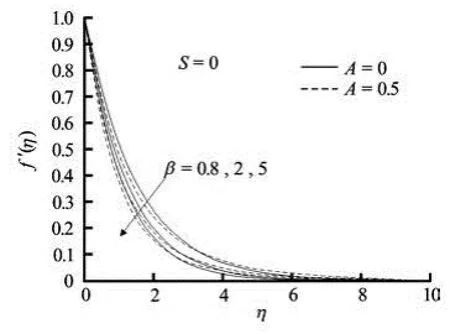
Fig.3(a) Velocity profiles for variable values of Casson parameter β for steady/unsteady motion in the absence of suction/blowing

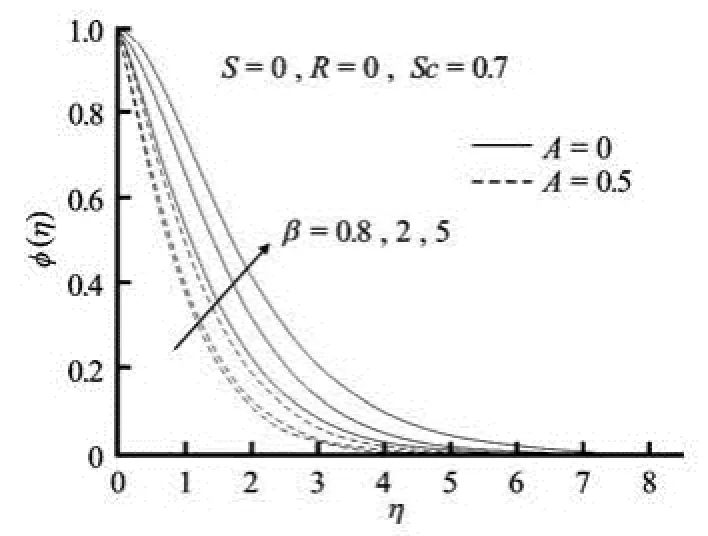
Fig.3(b) Concentration profiles for variable values of Casson parameter β for steady/unsteady motion in the absence of suction/blowing

The effects of Casson parameter β on the velocity and concentration profiles for both steady and unsteady flows in the absence of suction/injection are clearly exhibited in Figs.3(a)-3(b) respectively. For both steady and unsteady flows, the effect of increasing values of β is to reduce the velocity and hence the boundary-layer thickness decreases (Fig.3(a)). It is observed that ()fη′ and the associated boundarylayer thickness are decreasing functions of β. The velocity curves in Fig.3(a) show that the rate of transport is considerably reduced with the increase of β. The effect of increasing β is to enhance the concentration field for both steady and unsteady flows (Fig.3(b)). This effect is more pronounced for steady motion. The thickening of the solute boundary-layer occurs due to the increase in the elasticity stress parameter. It can also be seen from Fig.3(a) that the momentum boundary-layer thickness decreases as β increases, and hence results in an increase in the absolute value of the velocity gradient at the surface.

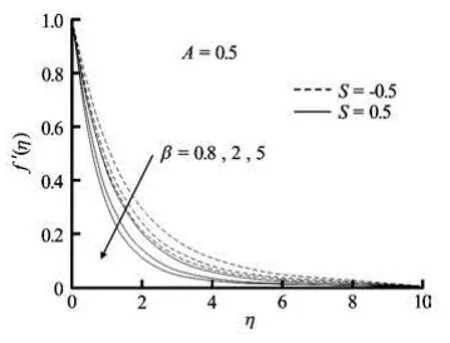
Fig.3(c) Velocity profiles for variable values of Casson parameter β for unsteady motion in presence of suction/blowing

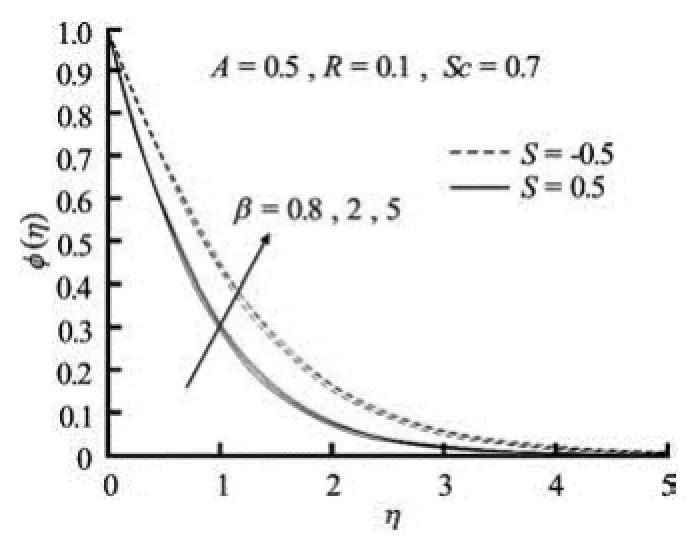
Fig.3(d) Concentration profiles for variable values of Casson parameter β for unsteady motion in presence of suction/blowing

Figures 3(c)-3(d) exhibit the changes in the velocity and the concentration fields for different values of the Casson parameter in the presence suction/injection for unsteady motion. Here also, fluid velocity decreases with increasing β for both cases of suction and injection (Fig.3(c)). Fluid velocity is much suppressed in the case of suction than that in the case of injection. However, the concentration increases in this case (Fig.3(d)).

The effects of suction/blowing parameter S on velocity and concentration fields are presented in Figs.4(a)-4(b) respectively. With increasing suction (0)S＞, fluid velocity is found to decrease (Fig.4(a)). That is, the effect of suction is to decrease the fluidvelocity in the boundary-layer and in turn, the wallshear stress decreases. The increase in suction causes thinning of the boundary-layer. However, the injection (0)S＜ has the opposite effect (Fig.4(a)). Concentration at a point is found to decrease with increasing S (Fig.4(b)). This causes a decrease in the rate of mass transfer. Quite opposite is the case for blowing (S＜0). The solute boundary layer is thinner in the case of suction (0)S＞ as compared to the case of impermeability (=0)S.

Fig.4(a) Velocity profiles for variable values of suction/blowing parameter S for unsteady motion

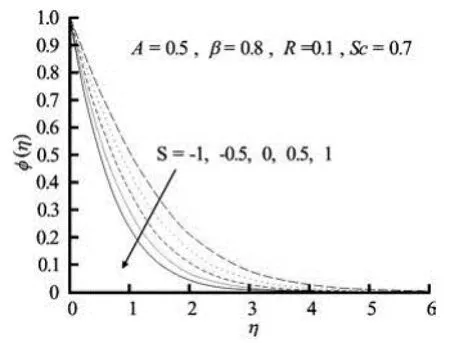
Fig.4(b) Concentration profiles for variable values of suction/ blowing parameter S for unsteady motion

Figures 5(a)-5(b) display the effects of reaction rate parameter R on concentration field in the presence suction and blowing respectively. In the case of constructive chemical reaction (0)R＜, concentration at a point on the sheet increases with increasing (absolute) values of the reaction rate parameter R for both cases of suction and blowing (Figs.5(a)-5(b)), whereas for destructive chemical reaction (0)R＞, the opposite behavior is noted, That is, the reactive solute distribution decreases with increasing R. In other words, the reaction-rate parameter is a decelerating agent in this case (Figs.5(a)-5(b)). As a result, the solute boundary layer becomes thinner. This is due to the fact that the conversion of the species takes place as a result of chemical reaction and thereby reduces the concentration in the boundary-layer (Figs.5(a)-5(b)). This effect is more pronounced in case of the blowing than that of the suction. The solute boundary-layer decreases in the case of destructive chemical reaction.

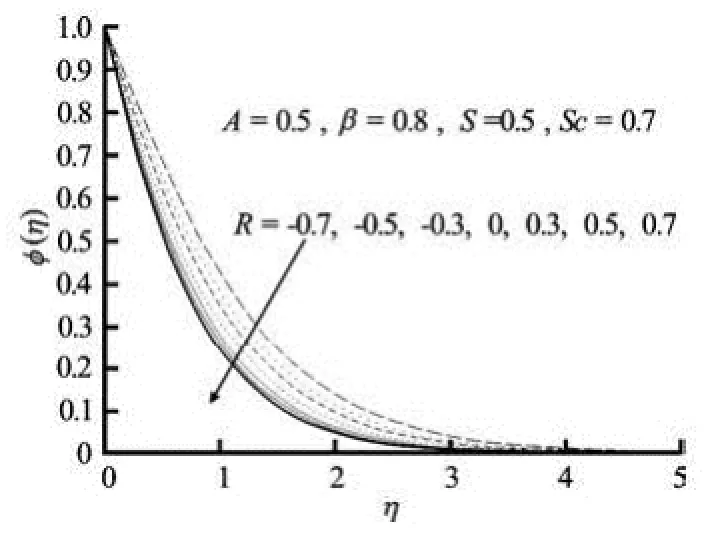
Fig.5(a) Concentration profiles for variable values of reaction rate parameter R in presence of suction

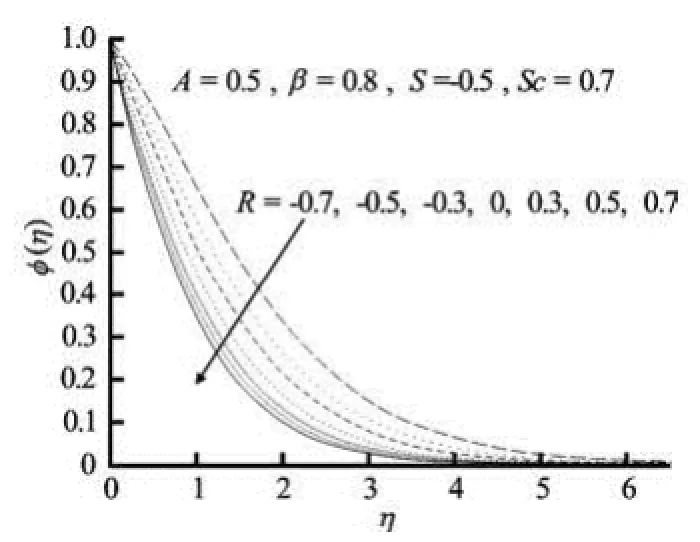
Fig.5(b) Concentration profiles for variable values of reaction rate parameter R in presence of blowing

The behavior of the concentration profiles for the variation of Schmidt number in the presence of suction and blowing can be found from Figs.6(a)-6(b) respectively. For both cases of suction and blowing, the concentration decrease with increasing Sc (Figs.5(a)-(b)). Moreover, the solute boundary-layer thickness decreases with increasing Schmidt numbers. The wall concentration gradient is negative for all values of the Schmidt number which means that the mass is always transferred from the surface to the ambient fluid. An increase in the Schmidt number reduces the solute boundary-layer thickness since the Schmidt number is inversely proportional to the diffusion coefficient D. Concentration field is much suppressed in the presence of suction than that of blowing.

Furthermore, the effects of unsteadiness parameter A and the Casson parameter β on (0)f′ (related to skin-friction coefficient) and (0)φ′ (related to mass transfer coefficient) in the absence of suction/blowing are presented in Figs.7(a) and 7(b). The magnitude of f′(0) decreases with increasing unsteadiness parameter A and also with the Casson parameter β, but the magnitude of mass transfer rate at the surface ((0))φ′decreases with β, increases with A. A drop in the skin friction as observed in this investigation has important applications to free coating operations, elastic properties of the coating formulations. This means that less force may be needed to pull a moving sheet at a given withdrawal velocity or equivalently higher withdrawal speeds can be achieved for a given driving force resulting from the increase in the rate of production.

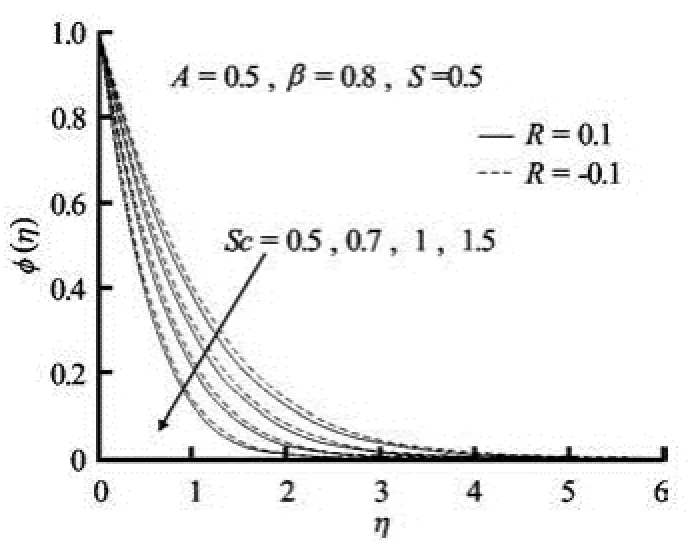
Fig.6(a) Concentration profiles for variable values of Schmidt number Sc in presence of suction

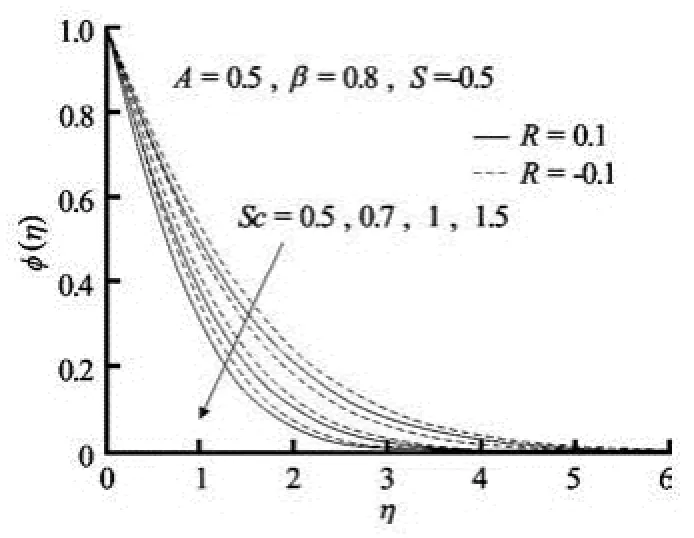
Fig.6(b) Concentration profiles for variable values of Schmidt number Sc in presence of blowing

Fig.7(a) Variation of (0)f′ related to skin-friction coefficient with Casson parameter β for three values of unsteadiness parameter A

Figures 7(c)-7(d) show the effects of suction/blowing on (0)f′ and (0)φ′. The magnitudes of both f′(0) and φ′(0) increase with increasing values of S. From Figs.7(a) and 7(c), it is very clear that f′(0) is negative. Physically, the negative sign of f′(0) implies that surface exerts a drag force on the fluid and positive sign implies the opposite. Wall concentration gradient ((0))φ′ decreases with increasing Sc, but increases in the case of constructive chemical reaction than that of destructive one (Fig.7(e)).

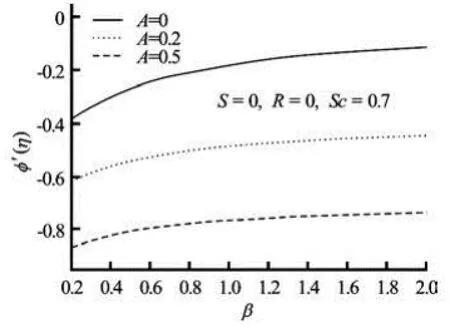
Fig.7(b) Variation of mass transfer coefficient with Casson parameter β for three values of unsteadiness parameter A

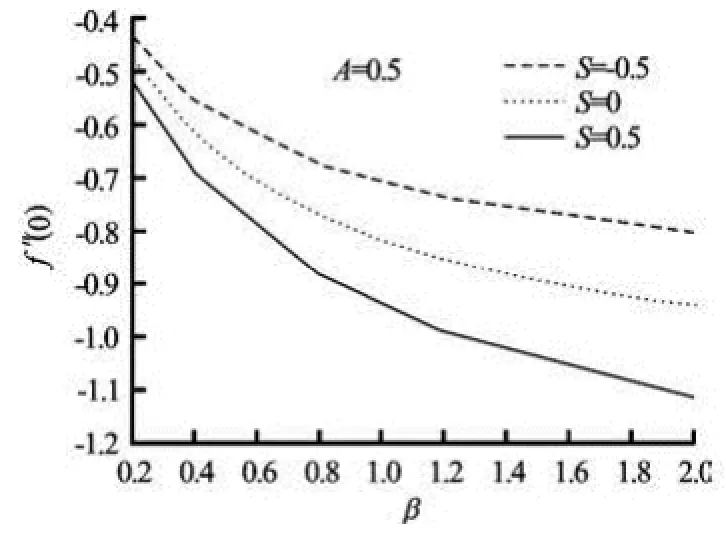
Fig.7(c) Variation of (0)f′ related to skin-friction coefficient with Casson parameter β for three values of suction/ blowing parameter S

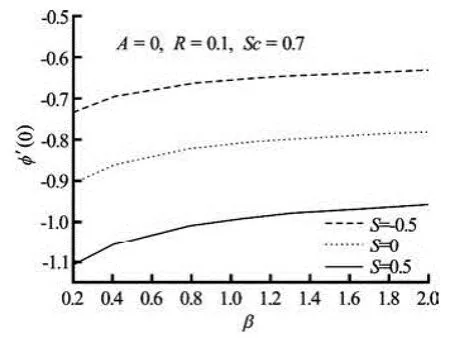
Fig.7(d) Variation of mass transfer coefficient with Casson parameter β for three values of suction/blowing parameter S

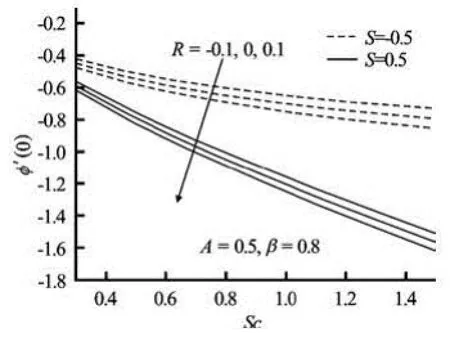
Fig.7(e) Variation of mass transfer coefficient with Schmidt number Sc for three values of reaction rate parameter R

5. Conclusion

The present study provides the numerical solutions for the boundary-layer flow and mass transfer of the Casson fluid over an unsteady permeable stretching surface in the presence of first order constructive/destructive chemical reaction. Fluid velocity decreases initially due to the increase in the unsteadiness parameter. In this case, the concentration decreases significantly. The effect of increasing values of the Casson parameter is to decrease the velocity field whereas the concentration is enhanced with increasing Casson parameter. The Schmidt number can be used to increase the rate of mass transfer. Moreover, an increase in the Schmidt number reduces the solute boundary-layer thickness. The solute boundary-layer thickness decreases in case of destructive chemical reaction.

Acknowledgement

We thank the reviewers for their constructive and helpful comments that led to definite improvement in the paper.

[1] CORTELL R. MHD flow and mass transfer of an electrically conducting fluid of second grade in a porous medium over a stretching sheet with chemically reactive species[J]. Chemical Engineering and Processing: Process Intensification, 2007, 46(8): 721-728.

[2] SIDDIQUI A. M., ZEB A. and GHORI Q. K. et al. Homotopy perturbation method for heat transfer flow of a third grade fluid between parallel plates[J]. Chaos, Solitons and Fractals, 2008, 36(1): 182-192.

[3] SAJID M., AHMAD I. and HAYAT T. et al. Unsteady flow and heat transfer of a second grade fluid over a stretching sheet[J]. Communications in Nonlinear Science Numerical Simulation, 2009, 14(1): 96-108.

[4] BOYD J., BUICK J. M. and GREEN S. Analysis of the Casson and Carreau-Yasuda non-Newtonian blood models in steady and oscillatory flow using the lattice Boltzmann method[J]. Physics of Fluids, 2007, 19(9): 093103.

[5] ANDERSSON H. I., AARSETH J. B. and DANDAPAT B. S. Heat transfer in a liquid film on an unsteady stretching surface[J]. International Journal of Heat and Mass Transfer, 2000, 43(1): 69-74.

[6] DANDAPAT B. S., SANTRA B. and VAJRAVELU K. The effects of variable fluid properties and thermocapillarity on the flow of a thin film on an unsteady stretching sheet[J]. International Journal of Heat and Mass Transfer, 2007, 50(5-6): 991-996.

[7] ALI M. E., MAGYARI E. Unsteady fluid and heat flow induced by a submerged stretching surface while its steady motion is slowed down gradually[J]. International Journal of Heat and Mass Transfer, 2007, 50(1-2): 188-195.

[8] SHARIDAN S., MAHMOOD T. and POP I. Similarity solutions for the unsteady boundary layer flow and heat transfer due to a stretching sheet[J]. International Journal of Applied Mechanics Engineering, 2006, 11(3): 647-654.

[9] MUKHOPADHYAY S. Effect of thermal radiation on unsteady mixed convection flow and heat transfer over a porous stretching surface in porous medium[J]. International Journal of Heat and Mass Transfer, 2009, 52(13-14): 3261-3265.

[10] MUKHOPADHYAY S. Effects of slip on unsteady mixed convective flow and heat transfer past a porous stretching surface[J]. Nuclear Engineering Design, 2011, 241(8): 2660-2665.

[11] CHAMKHA A. J., ALY A. M. and MANSOUR M. A. Similarity solution for unsteady heat and mass transfer from a stretching surface embedded in a porous medium with suction/injection and chemical reaction effects[J]. Chemical Engineering Communnications, 2010, 197(6): 846-858.

[12] BHATTACHARYYA K., MUKHOPADHYAY S. and LAYEK G. C. Slip effects on an unsteady boundary layer stagnation-point flow and heat transfer towards a stretching sheet[J]. Chinese Physics Letters, 2011, 28(9): 094702.

[13] HAYAT T., AWAIS M. and SAFDAR A. et al. Unsteady three dimensional flow of couple stress fluid over a stretching surface with chemical reaction[J]. Non-Linear Analysis: Modeling and Control, 2012, 17(1): 47-59.

[14] MUSTAFA M., HAYAT T. and POP I. et al. Unsteady boundary layer flow of a Casson fluid due to an impulsively started moving flat plate[J]. Heat Transfer–Asian Research, 2011, 40(6): 563-576.

[15] MUKHOPADHYAY S., VAJRAVELU K. Effects of transpiration and internal heat generation/absorption on the unsteady flow of a Maxwell fluid at a stretching surface[J]. Journal of Applied Mechanics, 2012, 79(4): 044508.

[16] MUKHOPADHYAY S. Unsteady boundary layer flow and heat transfer past a porous stretching sheet in presence of variable viscosity and thermal diffusivity [J], International Journal of Heat and Mass Transfer, 2009, 52(21-22): 5213-5217.

10.1016/S1001-6058(11)60400-X

* Biography: MUKHOPADHYAY Swati (1975-), Female, Ph. D., Assistant Professor

VAJRAVELU Kuppalapalle, E-mail: kuppalapalle.vajravelu@ucf.edu