污染環(huán)境下的隨機Logistic模型

關(guān)麗紅, 趙亞男

(長春大學(xué) 理學(xué)院, 長春 130022)

用微分方程描述一個簡單的Logistic模型通常表示為

(1)

其中:x(t)表示t時刻單個物種的生物種群密度;r0>0表示內(nèi)稟增長率;k>0表示環(huán)境容納量. 關(guān)于系統(tǒng)(1)的研究目前已有許多結(jié)果[1-4].

本文基于如下假設(shè)： 1) 無污染時種群按Logistic規(guī)律增長, 在污染環(huán)境中, 種群對毒素的劑量反應(yīng)取線性函數(shù), 毒素和種群間互相傳染; 2) 污染只通過環(huán)境影響種群, 如種群因呼吸受到毒害, 不計食物鏈的影響, 種群對毒素的吸入、 種群的排泄和自凈作用均取線性形式; 3) 環(huán)境的容量足夠大, 種群的吸收與排泄對環(huán)境毒素濃度的影響可忽略不計.

設(shè)x(t)表示時刻t種群的數(shù)量,C0(t)表示該時刻生物個體毒素體內(nèi)的濃度,CE(t)表示時刻t的環(huán)境毒素濃度,r0表示當不存在毒素時生物的內(nèi)秉增長率,r1表示生物增長對毒素的反應(yīng)強度,r0/k表示生物種群內(nèi)制約因子. 從而可得到生物增長滿足的方程:

dx(t)/dt=x(t)[r0-r1C0(t)-(r0/k)x(t)].

(2)

生物體內(nèi)毒素濃度的變化規(guī)律：

dC0(t)/dt=kCE(t)-gC0(t)-mC0(t),

(3)

其中:k,g,m為正常數(shù);kCE(t)表示時刻t生物對環(huán)境中毒素的吸收率, 設(shè)其與CE(t)成正比;gC0(t)表示時刻t對毒素的排除率;mC0(t)表示時刻t生物對毒素的凈化率.

環(huán)境中毒素濃度的變化規(guī)律如下：

dCE(t)/dt=-hCE(t)+u(t),

(4)

其中:h為正常數(shù);hCE(t)表示環(huán)境內(nèi)毒素的損失率;u(t)表示時刻t外界對環(huán)境的毒素輸入率, 是[0,+∞)上的非負連續(xù)有界函數(shù). 綜上, 可得污染環(huán)境的隨機Logistic模型：

初值條件為x(0)=x0>0, 0≤C0(0)<1, 0≤CE(0)<1. 把向環(huán)境中毒素的排放率函數(shù)u(t)作為系統(tǒng)的控制函數(shù). 考慮u(t)小于何值時, 系統(tǒng)是持久的,u(t)大于何值時, 系統(tǒng)將會滅絕. 確定性模型在某些情況下可以反映客觀世界污染環(huán)境中生物生長真實過程的一些重要特征. 可在多數(shù)情況下, 如果所考慮的種群個體數(shù)量不是很大, 隨機干擾強度和方差不是很小, 則只考慮確定性模型就不符合實際了, 此時把隨機干擾因素附加到模型中顯然更符合實際情況. 同時, 還要考慮到影響污染環(huán)境中生物生存或滅絕的關(guān)鍵因素, 才能使推導(dǎo)出的隨機模型更好地描述客觀實際情況[5-8].

dx(t)=x(t)[r0-r1C0(t)-(r0/k)x(t)]dt+αx(t)dBt,

(5)

初值條件為x(0)=x0>0, 其中Bt是一維標準Brown運動, 從而確定性的模型(M1)即變?yōu)槿缦码S機模型：

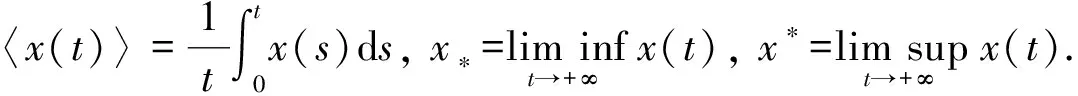
應(yīng)用文獻[9]的結(jié)果, 可得如下引理.

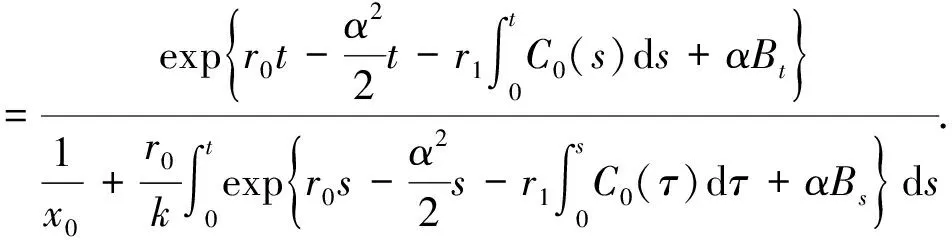
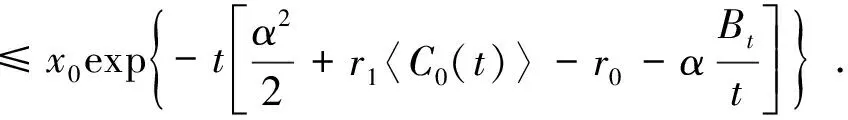
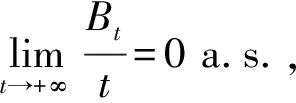
[1] May R M. Stability and Complexity in Model Ecosystems [M]. Princeton: Princeton University Press, 1973.

[2] Hallam T G, Zhien M. Persistence in Population Models with Demographic Fluctuations [J]. J Math Biol, 1986, 24(3): 327-339.

[3] HE Ji-wei, WANG Ke. The Survival Analysis for a Single-Species Population Model in a Polluted Environment [J]. Appl Math Model, 2007, 31(10): 2227-2238.

[4] HE Ji-wei, WANG Ke. The Survival Analysis for a Population in a Polluted Environment [J]. Nonl Anal: Real World Appl, 2009, 10(3): 1555-1571.

[5] JIANG Da-qing, SHI Ning-zhong, ZHAO Ya-nan. Existence, Uniqueness and Global Stability of Positive Solutions to the Food-Limited Population Model with Random Perturbation [J]. Math and Comput Model, 2005, 42(5/6): 651-658.

[6] ZHAO Ya-nan, WENG Shi-you. Existence and Uniqueness of Position Solutions to the General “Food-Limited” Species Model with Random Perturbation [J]. Journal of Jilin University: Science Edition, 2007, 45(6): 919-922. (趙亞男, 翁世有. 具有隨機擾動的廣義“食物有限”種群模型正解的存在性和唯一性 [J]. 吉林大學(xué)學(xué)報: 理學(xué)版, 2007, 45(6): 919-922.)

[7] ZHAO Ya-nan, GAO Hai-yin. Global Attractivity of Position Solutions to General “Food-Limited” Species Model with Random Perturbation [J]. Journal of Jilin University: Science Edition, 2011, 45(2): 263-266. (趙亞男, 高海音. 具有隨機擾動的廣義“食物有限”種群模型正解的全局吸引性 [J]. 吉林大學(xué)學(xué)報: 理學(xué)版, 2011, 45(2): 263-266.)

[8] JI Chun-yan, JIANG Da-qing, SHI Ning-zhong. Multigroup SIR Epidemic Model with Stochastic Perturbation [J]. Physica A: Statis Mech and Its Appl, 2011, 390(10): 1747-1762.

[9] JIANG Da-qing, SHI Ning-zhong, LI Xiao-yue. Global Stability and Stochastic Permanence of a Nonautonomous Logistic Equation with Random Perturbation [J]. J of Math Anal and Appl, 2008, 340(1): 588-597.