You want me to analyze data I don’t have? Are you insane?

Xiao-Li MENG

· Biostatistics in psychiatry (11) ·

You want me to analyze data I don’t have? Are you insane?

Xiao-Li MENG

Eighteen years ago, Professor Xinming Tu (one of the journal’s biostatistical editors) and I were coauthors of a paper[1]that involved missing data in chemometrics. One of the reviewer’s comments included the following:

The statement, ‘The naive approach of ignoring the missing data and using only the observed portion could provide very misleading conclusions’is nonsense to me (and I think the authors should also recognize it as nonsense in the real world). Similarly, what does it mean, ‘When analyzing such missing data, ...’; if the data are missing, you can't analyze them.

If you find nothing nonsensical in this reviewer’s comments, then the current article is worth a few minutes of your time. Statistical analysis has the same inductive nature as detective work: inferring unknowns from whatever one knows and observes, including the evidence that something is missing. Few qualified detectives would ignore suspicious absences in drawing their overall conclusions. Similarly, understanding the complications and consequences of having missing data is essential to reaching statistically meaningful and scientifically defensible conclusions.

1. Three complications when analyzing missing data

The first and most obvious complication with incomplete or missing data is the inapplicability of standard statistical methods and software, which are typically designed for ‘rectangular’ data. By ‘rectangular’, we mean an n by p data matrix where columns represent the p variables under study and rows the n individual subjects from whom we intended to collect data. All of us who have ever needed to handle a data matrix with ‘holes’ in it (i.e., missing data) have experienced frustration to one degree or another.

There is a crucial difference between a truly complete data matrix and one with holes, even when the holes are filled in by some imputation method. The difference lies in the amounts of information available for the intended analysis. With incomplete data there will be less information than when all intended data points are recorded as designed, even if the missing data is filled in by an imputation approach. This obvious fact is worth emphasizing because it stresses the importance of avoiding missing data at the design stage, to the extent possible, a point that is emphasized in the two previous articles in this series.[2,3]

The second complication is that once missing data occurs, our estimators will typically be less precise and our tests less powerful, compared to what we originally intended assuming a complete data set. In this situation simply increasing sample size to deal with the missing data will not guarantee more precise estimates or increased power; a probabilistically principled method would be needed, as detailed in Meng and Xie.[4]

The third and most critical complication, one that is far less commonly appreciated, is the potential for bias due to missing data. Even if the selected sample is perfectly representative of a targeted population,the missing data mechanism(MDM), that is, the process that is responsible for the loss of intended data, can severely compromise the representativeness or, more generally, the quality of data. This is because the MDM is essentially a sub-sampling step that is typically not under the control of the data collector. Rather, it is a self-selection process for reasons that often thoroughly violate the representativeness principle. Thus we may obtain very misleading conclusions if we analyze whatever passes through the MDM (i.e., the observed values) without questioning the reasons why some data were eliminated.

Several examples of the biases introduced by missing data were provided in the first article in this series.[2]Surveys of depression in China provide another example. Many individuals in China consider depressive symptoms a sign of a weak personality, not an indicator of a medical disorder that can be treated, so there is a strong tendency to under-report depressive symptoms. Howevernot reportingsymptoms is not the same asnot havingthem. This discrepancy has led to the puzzle, reported byScience,[5]that China has much lower rates of depression compared to those seen in Western countries, yet with comparable rates of suicide.

Not reporting a symptom or diagnosis can occur in two ways: a) the respondent skips the relevant question, or b) the respondent provides a false answer to the relevant question. Skipping the question – known asnon-response– occurs in essentially 100% of real-life surveys. Survey data with no missing data is almost certainly pre-processed data, not the original raw data. Whether or not you can still obtain valid statistical inferences from such preprocessed data depends on why the data were missing from the original raw data set and how appropriately the preprocessing step accounted for such reasons (to be discussed below).

Dealing with false answers is even more difficult because it requires us to first recognize that, although we appear to have a response, the real response is actually missing. The observed ‘no’ could be a real ‘no’, but it could also be a fake ‘no’ with the real answer being ‘yes’. We can never know for certain the correct answer for a particular individual, but there are various statistical methods that can be applied to reduce the potential biases in estimators of aggregate quantities (e.g., overall prevalence of depression in a population) as long as we can postulate reasonable assumptions about why respondents provide false negative answers.[6]

Although false answers might not be commonly recognized as a form of missing data, we include it to demonstrate that missing data problems arise in practice in many guises, some in the usual sense (e.g., nonresponses, censoring, truncation), and some in statistical modeling (e.g., latent variable model, hidden Markov models, counterfactuals in causal inferences). The statistical principles for dealing with missing data are essentially the same. We aim to reasonably capture the actual MDM, and ideally, incorporate it in our overall model. Minimally, we use our (often partial) knowledge of MDM to make appropriate adjustments to our complete-data procedures. After briefly discussing three common mistakes we will highlight three classes of methods for analyzing missing data.

2. Three common mistakes when handling missing data

Historically, the most common mistake when handling missing data is simply to drop any subject with any missing entry (e.g., individuals who did not answer all the questions will be removed from the database), adopting a so-calledcomplete-case analysis(CCA). The almost costless nature of this method – in terms of statistical modeling effort – has seduced many investigators, especially those with little statistical training. Fittingly, like many things in life, the lowest cost often comes with the lowest quality. The CCA method is guaranteed to be valid only when the missing data aremissing completely at random(MCAR[7]); that is, when the MDM is completely determined by random chance alone, as discussed by Lin and colleagues[2]. This is a very restrictive assumption which can rarely be justified in practice, because missing data typically occur for particular reasons, not just by chance. For the aforementioned depression example, dropping all the cases with nonresponses, which are more likely, to occur among those who actually suffer from depression can only reinforce the misleading inference that the prevalence of depression is very low. Mounting literature demonstrating the serious biases from conducting CCA,[8,9]has led to the substantial decrease in inappropriate use of CCA though by no means has it ceased.

The second common mistake is to simply fill in the missing entries by some convenient values (e.g., sample averages) or, perhaps more sophisticatedly, with a regression prediction based (solely) on the observed data (e.g., via fitting a regression model using the complete cases). Suchmean or regression imputationmethods aim to improve upon the CCA method by retaining more data and attempting to predict the missing data in some reasonable way. Unfortunately, such methods still do not correct for missing-data bias in general, because these missing-data imputations themselves may be based on a biased sample. There are, however, special cases where such methods can lead to valid point estimators: when one can assume data aremissing at random(MAR)[7]the mean or regression imputation process for linear estimators can use the MAR property (e.g., the mean imputation can be performed separately for the two gender groups or the regression imputation can use gender as a covariate).

But as soon as we move beyond linear statistics, analyzing a single set of imputed data as if they were real cannot even lead to correct point estimators. For example, when we fill in each missing entry by some kind of mean and then compute a sample variance based on such data, it will underestimate the actual variance. This occurs because we have artificially eliminated some natural variability by replacing a missing data point by an estimate of its mean, which has less variability. Similarly, estimates of correlations are distorted because a correlation between variables can be very different from the correlation of their means – mistaking the two as the same is known as theecological fallacy.[10]There have been many studies[11]that demonstrate the problems of mean and regression imputations in real-life problems.

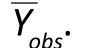
3. Three classes of methods for analyzing missing data

The first class of methods for analyzing missing data– non-parametric methods – can be employed when a missing data problem can be treated as a problem of dealing with unequal probability sampling. For example, when the bias caused by MDM can be handled by adjusting for non-response rates, then reweighting (a non-parametric method) can be quite effective. A simple example illustrates this point. Suppose that on a question about the use of mental health services, men’s response rate was only half of women’s response rate, and that upon further investigation we convinced ourselves that we can treat the MDM as MAR[7]with gender as the only relevant predictor of missingness. Then, to estimate the rate of service use for the overall population, we can simply give each male respondent a weight proportional to 2 (i.e., the inverse of the probability of response, [1/0.5]), while each female respondent receives a weight proportional to 1, and then compute the weighted average. This will effectively restore the correct gender balance of the original complete sample (i.e., as if everyone had responded) and lead to an (approximately) unbiased estimator. This estimator’s variance can be calculated using the variance formula for a ratio estimator.

The method of weighting by the inverse of the probability of response has been generalized to more complicated situations, especially with the use of estimating equations,[13]but the underlying principle remains the same. The major drawback of this class of methods is the large variances of the estimates that occur because of the small values of the probability of response appearing in the denominators of the weights, a well-known problem for the so-called Horvitz-Thompson estimators.[12]The method’s main advantage is it avoids explicitly modeling how MDM depends on the observed quantities. Note that this class of reweighting methods can be justified only when the MDM is MAR. If the MDM depends on any unobserved quantity, then the response probability cannot be directly estimated or assessed from the observed data themselves. In such cases, further (unverifiable) modeling assumptions are needed in order to proceed.

The second class of methods for analyzing missing data – parametric methods – makes parametric distributional assumptions about the complete data and the MDM. Note here that the observed data include both the observed sample values and a missingdata indicatorRthat specifies whether the data point is missing or observed. In the previously discussed simple random sampling setting if we letRi=1 whenYiis observed andRi=0 whenYiis missing, then the model forR conditional onYallows us to capture the MDM. In the simple random sampling setting, if the MDM is MCAR then this conditional model is simply a Bernoulli model forRiwith the probability of response independent of the value ofYi. In contrast, if the MDM is not MCAR, then the probability of response (p) can vary withYi. For example, the logit of p could decrease linearly withYi, in which case the response probability decreases with the value ofYi(e.g., a person with higher usage of mental health services tends to have a lower probability of reporting). See Little and Rubin[14]for examples with various degrees of complexity. Once such a model is in place, we can proceed by using the maximum likelihood estimator (MLE) or by Bayesian analysis if we are also willing to specify a ‘prior’ for the model parameters. Such priors are vital when the parameters for MDM are not identifiable from the observed data alone. A key advantage of this parametric modeling approach is its efficiency, when the specified model (including for MDM) is acceptable. Otherwise the estimates are biased even asymptotically (that is, even when we have an infinite amount of data). This is a case of the standard bias-variance trade-off.

The computation of the MLE from the observeddata likelihood is typically difficult to carry out directly. A very popular iterative algorithm, the EM algorithm[15](with many generalizations and variations[16]) handles such problems, especially when the MDM is MAR. For Bayesian computation, there is a whole class of Markov chain Monte Carlo (MCMC) methods,[17]including the stochastic counterpart of the EM algorithm and its generalizations, such as the Data Augmentation (DA) algorithm and more generally the Gibbs Sampler, as reviewed in van Dyk and Meng.[18]

The third class of methods for analyzing missing data – imputation methods – are popular because once the missing values are filled in, the standard completedata procedures and software can be applied (but this does not imply that the corresponding results are valid).Typically a central goal of an imputation method is to eliminate the holes in a database so subsequent users can employ their favorite complete-data models. The quality of imputation is crucial: we all understand the common-sense axiom "garbage in, garbage out". Even if we have an ideal imputation method, one that exactly captures the MDM, the imputed data are still not real, and therefore we need to adjust our analysis to reflect the uncertainty inherent in the imputation. For single imputation, when each missing value is imputed only once, we need specially-designed procedures to handle different estimators.[19]

Multiple imputation[20]addresses this problem by providing several imputations for each missing value, creating replications that allow for variance estimation directly from the imputed values. Specifically, Rubin’s[20]multiple imputation (MI) first builds a comprehensive imputation model for all the missing values as a set, a task usually too cumbersome for an individual analyst and hence usually completed by the data collection agency (e.g., a census bureau). The analyst then uses this model to drawmindependent imputations, creatingmcompleted-datasets which are then analyzed by repeating the intended complete-data analysismtimes. The MI estimator is then simply the average of theirmcomplete-data estimators (e.g., regression coeffecient), and its variance is obtained via the so-called Rubin’s variance combining rule, which adds up the withinimputation variance and the between-imputation variance (both of which are trivial to compute from themsets of analysis outputs). Complications exist when the analysis procedure is not compatible with the model used to draw the imputations, but even in such cases, MI is still a viable and sometimes preferred strategy; see Meng[21]and Xie and Meng[22]for discussions and investigations.

4. Three questions to ask whenever facing missing data

Whenever we face missing data, which is essentially all the time in practice, it is worthwhile to ask ourselves the following three questions:

1) Why are data missing?

2) Do the missing data really make any difference?

3) Have I done the best that I could to handle the missing data?

The first question is the most fundamental for the reasons outlined above. Even if we cannot answer the question, and in most cases we cannot or do not have a complete answer, simply raising the question helps to remind ourselves that our final results, no matter how sophisticated they may appear, may suffer from a serious nonresponse bias. Our conclusions may apply only to a subpopulation that is very different from our original intended population because our observed sample is self-selected. Consequently, even if we do not know why the data are missing or do not know how to model the MDM, we should at the least acknowledge this potential bias when we present the results of our analysis.

The second question is a practical one. Yes, almost every real-life problem comes with some missing data. But if the amount ofmissing informationis small, then perhaps our inferences would not be that different even if we had observed all the data. Note here we use the terminformationinstead ofdatabecause the two quantities are not necessarily the same. A small amount of missing data almost always implies a small amount of missing information, but not vice versa. Consider a two-question survey in which the answer to the first question is highly correlated with the answer to the second question. Even if very few subjects answer the first question (perhaps due to its sensitive nature), as long as most people answer the second question (a good proxy to the first question that does not appear to be as sensitive), we may have a limited loss of information. In such cases,for practical purposes, it may be acceptable to adopt a simplistic method for handling the missing data (e.g., ignore the first question), especially when facing time constraints. However, even if we choose to ignore missing-data because we truly believe that it would not alter our practical conclusions, we should still explicitly acknowledge the choice we have made. This is not merely for scientific integrity, but also to acknowledge the possibility that we were overly confident because we overlooked certain issues that would be more apparent to others.

The third question is to make ourselves consider if we could have extracted more information out of the data available. In mental health and other medical studies, collecting data can be expensive and there is great incentive to get as much information out of our data as possible. At the same time, we want to be sure that the conclusions we draw from the information we obtain are not misleading. The best way to simultaneously achieve these two goals, to the largest extent possible, is to carefully model the distribution of the observed values and the missing-data indicators, and to then follow a probabilistically principled method, be it parametric or non-parametric, to arrive at our inference. We can never be certain that we have captured all the intricacies of the underlying MDM, but it is certain that by simply ignoring the missing data our final analysis will suffer from either nonresponse bias or inefficiency and, most likely, both. In this sense, analyzing the data we do not have reflects the soundness of our statistical mind, and the more we can put into this endeavor, the more we can advance science and civilization.

Acknowledgments

I thank Alex Blocker, Radu Craiu, Steven Finch, and Xianchao Xie for very helpful comments and proofreading, and NSF for partial financial support.

1. Tu XM, Meng XL, Pagano, M. On the use of conditional maximization in chemometrics.J Chemom1994; 8(5): 365-370.

2. Lin JY, Lu Y, Tu X. How to avoid missing data and the problems they pose: Design considerations.Shanghai Arch Psychiatry2012; 24(3): 181-184.

3. Biswas K. Prevention and management of missing data during conduct of a clinical study.Shanghai Arch Psychiatry2012; 24(4): 235-237.

4. Meng XL, Xie X. I got more data, my model is more refined, but my estimator is getting worse! Am I just dumb?Econometric Reviews2013.(in press)

5. Miller G. China: Healing the metaphorical heart.Science2006; 311(5760): 462-463.

6. Liu J, Meng XL, Chen CN, Alegria M. Multiple imputation for response biases in NLAAS due to survey instruments.Proceedings of the Survey Research Methods Section of the American Statistical Association2006; 3360-3366.(CD-ROM)

7. Rubin DB. Inference with missing data.Biometrika1976; 63, 581-592.

8. Demissie S, LaValley MP, Horton NJ, Glynn RJ, Cupples LA. Bias due to missing exposure data using complete-case analysis in the proportional hazards regression model.Stat Med2003; 22(4): 545-57.

9. Liu F. Estimation bias in complete-case analysis in crossover studies with missing data.Commun Stat Theory Methods2011; 40(5): 812-817.

10. Goodman L. Ecological regression and the behavior of individuals.Am Socio Rev1953; 18, 663-64.

11. Barrzi F, Woodward M. Imputations of missing values in practice: Results from imputations of serum cholesterol in 28 cohort studies.Am J Epidemiol2004; 160(1): 34-45.

12. Cochran WC.Sampling Techniques, 3rd ed. New York: Wiley, 1977.

13. Lipsitz SR, Ibrahim JG, Zhao LP. A weighted estimating equation for missing covariate data with properties similar to maximum likelihood.J Am Stat Assoc1999; 94(448): 1147-1160.

14. Little RJA, Rubin DB.Statistical Analysis with Missing Data. New York: Wiley, 2002.

15. Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm.Journal of the Royal Statistical SocietySeries B1977; 39(1): 1-38.

16. Meng XL, van Dyk DA. The EM algorithm – An old folk-song sung to a fast new tune (with discussion).Journal of the Royal Statistical SocietySeries B1977; 59(3): 511-567.

17. Brooks S, Gelman A, Galin J, Meng XL.Handbook of Markov chain Monte Carlo. London: Chapman and Hall/CRC, 2011.

18. van Dyk DA,Meng XL. Cross fertilizing strategies for better EM mountain climbing and DA field exploration: A graphical guide book.Statistical Science2010; 25(4): 429-449.

19. Schafer JL, Schenker N. Inference with imputed conditional means.J Am Stat Assoc2000; 95(449): 144-154.

20. Rubin DB.Multiple Imputation for Nonresponse in Surveys. New York: Wiley, 1987.

21. Meng XL. Multiple-imputation inferences with uncongenial sources of input (with discussion).Statistical Science1994; 9(4): 538-573.

22. Xie X, Meng XL. Exploring multi-party inferences: What happens when there are three uncongenial models involved?Journal of the Royal Statistical SocietySeries B(under review by)

Xiao-Li Meng is the Whipple V. N. Jones Professor of Statistics and the Dean of the Graduate School of Arts and Sciences at Harvard University, and a faculty member of the Center of Health Statistics at the University of Chicago. His research interests include statistical inference with incomplete data, quantifying information in scientific studies, effective statistical computational methods including EM-type algorithms and MCMC methods, statistical foundational issues, and statistical applications in natural, social and medical sciences. He served as a statistical consultant on a number of projects on mental health status of and service usage by Asian and Latino populations in the United States, resulting in (joint) publications in American Journal of Psychiatry, Psychiatric Services, and other leading psychiatric journals.

10.3969/j.issn.1002-0829.2012.05.011

Department of Statistics, Harvard University, Boston, USA

*correspondence: mengharvard@gmail.com