一類雙調(diào)和映照的單葉半徑估計
夏小青,黃心中
(華僑大學(xué)數(shù)學(xué)科學(xué)學(xué)院,福建泉州 362021)
一類雙調(diào)和映照的單葉半徑估計
夏小青,黃心中
(華僑大學(xué)數(shù)學(xué)科學(xué)學(xué)院,福建泉州 362021)
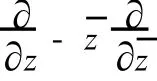
,即L是一個線性復(fù)算子.利用單位圓上有界調(diào)和函數(shù)的系數(shù)估計不等式,對雙調(diào)和映照L(F)的單葉半徑進(jìn)行估計,所得到的結(jié)果優(yōu)于Chen和Ponnusamy等的結(jié)果.
Landau定理;雙調(diào)和映照;線性復(fù)算子;單葉半徑
1 預(yù)備知識

單連通區(qū)域D上的雙調(diào)和映照F=r2G+K.其中:G,K均為D上的調(diào)和映照[1].D上的調(diào)和映照G,K又可表示為:G=g1+,K=k1+.其中:g1,g2,k1,k2都是D上的解析函數(shù)[2].若單位圓D={z||z|<1}上的雙調(diào)和映照F,可表示為F=r2G+K滿足F(0)=K(0)=0,JK(0)=1,且|G(z)| 定理A 假設(shè)F=r2G+K是單位圓D={z||z|<1}上的雙調(diào)和映照,且滿足F(0)=K(0)=0, JK(0)=1.其中:G,K都是D上的有界調(diào)和映照.|G(z)| 定理B 假設(shè)F=r2G是單位圓D={z||z|<1}上的雙調(diào)和映照,且滿足G(0)=0,JG(0)=1.其中:G是D上的有界調(diào)和映照,|G(z)| 的解.其中:m1同定理A,L(F)(Dρ2)包含一個單葉圓DR,有 繼續(xù)對以上兩個定理的單葉半徑問題進(jìn)行研究,進(jìn)一步估計L(F)的單葉半徑,改進(jìn)了文獻(xiàn)[4]相應(yīng)的結(jié)果. 單位圓D={z||z|<1}上的復(fù)值函數(shù)f的Jacobian記為Jf,即Jf=|fz|2-|fˉz|2.記λf=||fz|-|fˉz||,Λ=|fz|+|fˉz|.若f是調(diào)和映照,Lew y[5]指出,它是局部單葉的當(dāng)且僅當(dāng)Jf(z)≠0,z∈D. 引理B[8]假設(shè)f(z)=h(z)+是單位圓D上的調(diào)和映照,h,g是D上的解析函數(shù),具有冪級.如果Jf(0)=1,|f(z)| 定理1 假設(shè)F=r2G+K是單位圓D={z||z|<1}上的雙調(diào)和映照,且滿足F(0)=K(0)=0, JK(0)=1.其中:G,K都是D上的有界調(diào)和映照,且|G(z)| 的解,且L(F)(Dρ3)包含一個單葉圓DR,有 下面證明H(z)的單葉性問題. 固定0<ρ<1,要證明H在Dρ上的單葉性,任取Dρ上的兩點(diǎn)z1,z2,用γ表示線段[z1,z2],則有 從證明的過程中可看出,定理1中的ρ3一定比定理A中的ρ1大,從而定理1的結(jié)論比定理A的結(jié)論好.相應(yīng)于定理B,有如下定理. 定理2 假設(shè)F=r2G是單位圓D={z||z|<1}上的雙調(diào)和映照,且滿足G(0)=0,JG(0)=1.其中:G是D上的有界調(diào)和映照,|G(z)| 的解,且包含一個單葉圓有 [1]ABDULHAD IZ,MUHANNA Y A,KHURIS.On some properties of solutions of the biharmonic equation[J].Appied Mathematics and Computation,2006,177(1):346-351. [2]DUREB P.Harmonic mappings in the plane[M].Cabridge:Cabridge Univ Press,2004. [3]ABDULHAD IZ,MUHANNA Y A.Landau′s theorem for biharmonic mappings[J].J Math Anal Appl,2008,338 (1):705-709. [4]CHEN S.PONNUSAM Y S,WANG X.Landau′s theo rem for certain biharmonic mappings[J].App lied Mathematics and Computation,2009,208(2):427-433. [5]LEW Y H.On the non-vanishing of the Jacobian in certain one-to-one mappings[J].Bull Amer Math Soc,1936, 42(10):689-692. [6]CHEN H H,GAU TH IER PM,HENGARTNERW.Bloch constants for planar harmonic mappings[J].Proc Amer Math Soc,2000,128(11):3231-3240. [7]HUANG Xin-zhong.Estimates on Bloch constants for planar harmonic mappings[J].J Math Anal Appl,2007,337 (2):880-887. [8]LIU Ming-sheng.Landau′s theorem for planar harmonic mappings[J].Computers and Mathematics with Appications,2009,57(7):1142-1146. [9]LIU Ming-sheng.Estimates on bloch constants for planar harmonic mappings[J].Science in China Series(A): Mathematics,2008,52(1):87-93. [10]LIU Ming-sheng.Landau′s theorems for biharmonic mappings[J].Com lex Variables and Ellip tic Equations, 2008,53(9):843-855. (責(zé)任編輯:陳志賢英文審校:張金順,黃心中) On the Estimates of Univalen t Radius for Certain Biharmonic Mappings XIA Xiao-qing,HUANG Xin-zhong landau theorem;biharmonic mapping;linear complex operator;univalent radius O 174.5 A 1000-5013(2011)02-0218-05 2009-10-11 黃心中(1957-),男,教授,主要從事函數(shù)論的研究.E-mail:huangxz@hqu.edu.cn. 福建省自然科學(xué)基金項(xiàng)目(2008J0195)
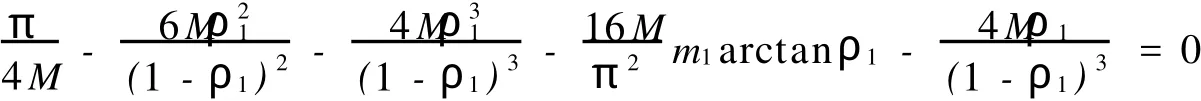


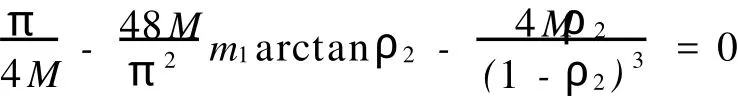
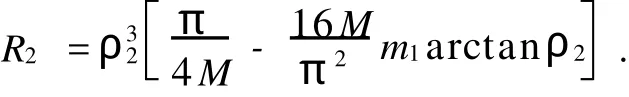

2 主要結(jié)果及證明

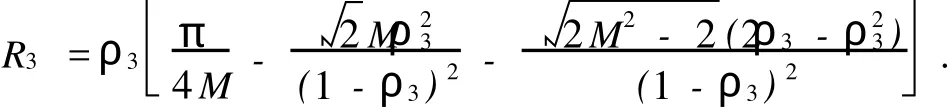





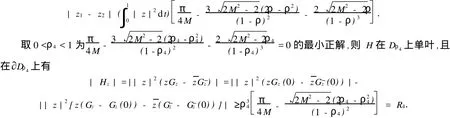
(School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)