岳崇山,宋旭華,景海斌

(1.河北北方學(xué)院理學(xué)院,河北張家口075000;2.宣化科技職業(yè)學(xué)院數(shù)學(xué)系,河北宣化075100;3.河北建筑工程學(xué)院數(shù)理系,河北張家口075000)

研究平面區(qū)域的邊界曲線的局部軸對稱性是比較和測量平面或空間區(qū)域的外形的諸多方法中極為重要的一種方法.即給定平面上的簡單光滑閉曲線M,研究與M相切不止一點的圓.如果M上每一點都存在這樣的圓,那么就表明平面曲線具有 “局部”的對稱性:切線和切點關(guān)于一條曲線對稱.所有這些雙切圓的中心形成軌跡稱為M的對稱集(它與中軸,對稱軸變換,中心集等密切相關(guān)).在平面區(qū)域的外形識別中,這個集合有著非常重要的作用.關(guān)于這方面的研究見參考文獻(xiàn)[1-4].

Peter J.Gibin和Donal B.O＇shea討論了平面閉曲線的雙切圓的存在性問題[5,6].他們的論文中,切割函數(shù)是一個重要的概念和工具.但是他們定義的切割函數(shù)僅適用于閉曲線,實際上切割函數(shù)是可以定義在一般的曲線上的.本文的工作就是在重新定義切割函數(shù)之后,討論切割函數(shù)的分析特性,即連續(xù)性和可導(dǎo)性.

1 基本概念

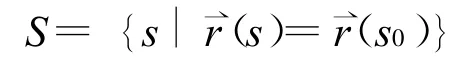
定義 1.1[7,8]設(shè)(s)={x(s),y(s)}平面曲線,稱(s)={-y＇(s),x＇(s)}為曲線的單位法向量.

定義1.2 設(shè) r(s)為平面曲線,κ(s)為其相對曲率,r(s0)是曲線上一點.稱

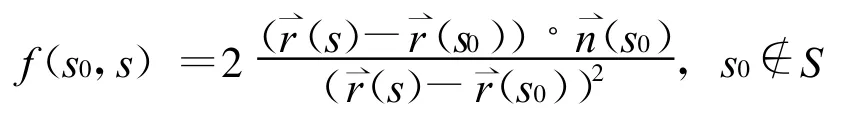
為曲線r(s)的切割函數(shù),

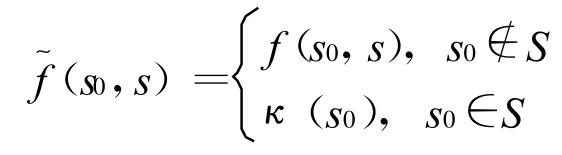
為曲線r(s)的拓廣的切割函數(shù).

2 主要結(jié)果

考察平面曲線的拓廣的切割函數(shù)的分析性質(zhì).關(guān)于分析性質(zhì)的定義參見文獻(xiàn) [8],向量函數(shù)的分析性質(zhì)的定義見參考文獻(xiàn) [9,10].下面的定理考察了平面的曲線的拓廣的切割函數(shù)的連續(xù)性.

定理2.1 平面曲線的拓廣的切割函數(shù)是連續(xù)函數(shù).

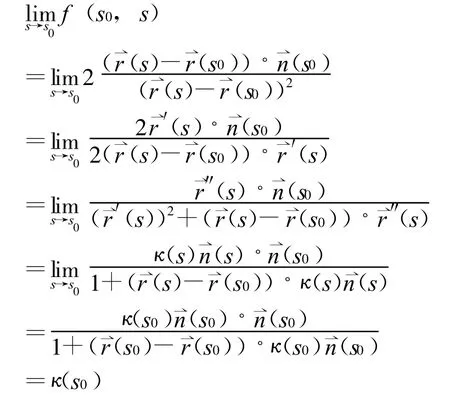
下面的定理考察了平面的拓廣的切割函數(shù)的可導(dǎo)性.

定理2.2 如果平面曲線是Cm(m≥2)類的,那么適當(dāng)?shù)匮a(bǔ)充值之后,其拓廣的切割函數(shù)是類的C(m-2).

證明 當(dāng)s0?S時,由于平面曲線r(s)是Cm類的,而其拓廣的切割函數(shù)的表達(dá)式為

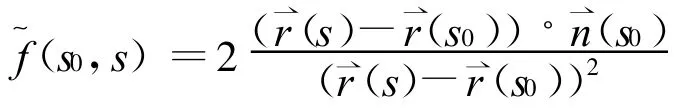
設(shè) r(s)={x(s),y(s)},點 P0(s0)處的參數(shù)值為 s0=0,(s0)=, 單位切向量′(s0)的方向為 x軸的正向.(s0),′(s0)和單位法向量n(s0)一起構(gòu)成單位右手標(biāo)架.在s0鄰近,曲線的切割函數(shù)按其分量展開為

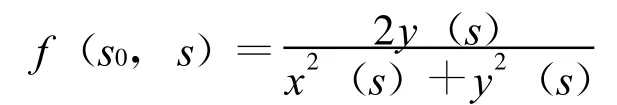
由于曲線 r(s)是 Cm(m≥2)類的,則它在s0鄰近的泰勒展開為

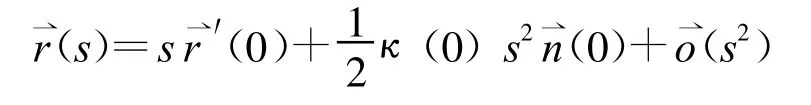
因而在s0鄰近有

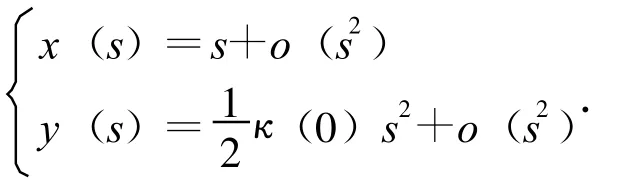
將其帶入到切割函數(shù)的表達(dá)式中有

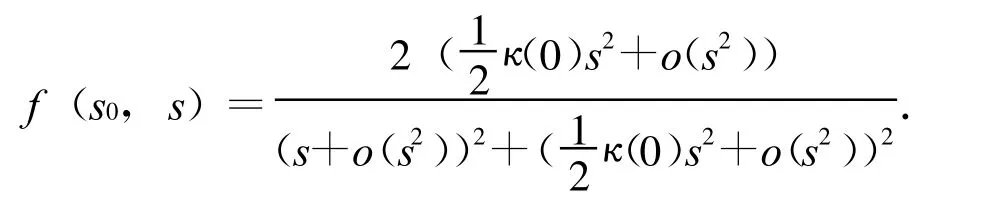
由于新的表達(dá)式中,分子分母都是C(m-2)類的,且分母有意義,故適當(dāng)?shù)匮a(bǔ)充值可以使得拓廣的切割函數(shù)(s0,s)是C(m-2)類的.

由定理2.1和定理2.2立即可得下面的推論.

推論2.1 如果平面曲線是光滑的,那么其拓廣的切割函數(shù)也是光滑的.

3 小 結(jié)

本文主要討論了平面曲線的拓廣的切割函數(shù)的分析性質(zhì),包括連續(xù)性和光滑性.進(jìn)一步地,空間曲線的拓廣的切割函數(shù)是否具有相同的性質(zhì)?這個問題將是我們進(jìn)一步的研究工作.

[1]Blum H.Biological shape and visual science[J].J Theoret Biol,1973,38:205-287

[2]Brady M.Criteria for representations of shape[M].New York:Academic Press,1983.23-34

[3]Bruce M,Giblin PJ,Gibson CG.Symmetry set[J].Proc Royal Soc 1985,101A:163-186

[4]Giblin PJ,Brassett SA.Local symmetry of plane curves[J].Amer Math Monthly,1985,92:689-707

[5]Gibin PJ,O'shea DB.The Bitangent Sphere Problem[J].Amer Math Monthly,1990,97(01):5-23

[6]Gelman A,Carlin JB,Stern HS,et al.Bayesian Data Analysis(2nd ed)[M].Boston:Chapman Hall/CRC,2004,45-67

[7]Rutter JW.Geometry of Curves[M].Boston:Chapman and Hall/CRC,1935,56-231

[8]張筑生.數(shù)學(xué)分析新講(第一冊)[M].北京:北京大學(xué)出版社,1990:78-98

[9]梅向明,黃敬之.微分幾何(第二版)[M].北京:高等教育出版社,2003:4-90

[10]陳維桓.微分幾何[M].北京:北京大學(xué)出版社,2006:75-109