Weighted Markov chains for forecasting and analysis in Incidence of infectious diseases in jiangsu Province, China☆
Zhihng Peng, Chngjun Bo, Yng Zho, Honggng Yi, Letin Xi, Ho Yu, Honging Shen,Feng Chen*
aDepartment of Epidemiology and Biostatistics, Nanjing Medical University School of Public Health, Nanjing 210029,Jiangsu Province, China
bCenter for Disease Control and Prevention of Jiangsu Province, Nanjing 210029, Jiangsu Province, China
cApplied Mathematics Department, Hohai University, Nanjing 210029, Jiangsu Province, China
INTRODUCTION
Mathematical models of any natural phenomenon should rest on some basic knowledge of the phenomenon and the data collected to track and understand it. Many years ago, J.L.Doob had defined a"stochastic process" as the mathematical abstraction of an empirical process whose development is governed by probabilistic laws. It is important to note that the term "stochastic process" refers to the mathematical abstraction, model, or representation of the empirical process and not to the empirical process itself. During recent years, the theory of stochastic process has developed very rapidly and has found application in a large number of fields[1].
In particular, a class of stochastic processes termed Markov chains or processes has been investigated extensively. Markov chains are one of the richest sources of models for capturing dynamic behavior with a large stochastic component[2,3]. It is of great importance in many branches of science and engineering and in other fields, including physics[4,5],industrial control[6,7], reliability analysis[8], optimality analysis[9], economics[10,11], etc. The Markov chains theory is a method of making quantitative analysis about the situation in which the system transfers from one state to another, hence predicting future tendencies. This provides a basis for making strategic analysis.
In the field of medicine and public health, the occurrence, development and prognosis of a disease will inevitably be affected by external factors and the human body factors. As these factors are closely interrelated with one another, it is difficult to explain them in a structural causal model. However, it is the interdependent relation between these data that is the most important and useful characteristic of the research objectives[12]. Here, it will be an effective way for us to establish a dynamic model in time order according to the change law of the disease.
In the past, many scholars have applied the Markov chain theory to forecast the incidence of infectious diseases, and established some corresponding mathematical models. In this way, various types of infectious diseases can be analyzed and studied comprehensively using the Markov chain theory.Markov processes have been applied in the study of the AIDS[13-15], contraceptives[16], ecology[17], cancer[18]and other diseases[19,20]. Depending on the particular conditions of each study, different methodologies have been used. At the same time, different Markov models have been used in biomedical data analysis, especially for epidemiology research[21-25].
In this paper we will look at the use of Markov models for forecasting and analysis in the specific field of incidence of infectious diseases. These methods of quantitative analysis enjoy wide popularity because they are less dependent on historical data, have comparatively high accuracy and extensive adaptability. However, this kind of forecasting analysis based on the traditional Markov chain theory is destined to have defects and flaws.The homogeneity of the Markov chain has yet to be proved. There is enormous difficulty associated with adjusting the transition probability matrix, and the accuracy of the forecast is affected by objective factors.
This article attempts to overcome all these difficulties, and to establish a mathematical model to forecast the infectious diseases based on the weighted Markov chain theory. The authors will both leverage the advantages of the traditional Markov chain theory,and using the correlation analysis approach and historical data, seek more in-depth analysis of the usual characteristics that exist in the occurrence of the infectious diseases. These characteristics include longterm trends, seasonal characteristics, periodicities,short-term fluctuations and irregular variations.
The remainder of the paper proceeds as follows.The method of sequential cluster is described in Section 2. In Section 3 we describe the idea of weighted Markov chains. Markov chain Monte Carlo (MCMC)methods are considered in Section 4. Section 5 presents an application using real data from Jiangsu Province, and Section 6 contains some concluding remarks.
ONE-DIMENSIONAL SEQUENTIAL CLUSTER ANALYSIS
Cluster analysis involves techniques that produce classifications from data that are initially unclassified,and should not be confused with discriminant analysis,where the number of existing distinct groups and corresponding data are known. There are two basic ways to search for clusters. These two methods are differentiated and categorized as either hierarchical or nonhierarchical in nature[26]. A variety of hierarchical clustering techniques have been implemented and successfully used to analyze or cluster onedimensional and high-dimensional data[27-29]. Based on the characteristic of infectious disease incidence data,this paper attempts to only use the one-dimensional sequential cluster analysis algorithm to measure off the incidence data by SAS software.
To classify the one-dimensional sequential samples,partition points in the sequential series of samples are identified and the samples are then divided into several sections. Each section is unique, and this kind of classification can be called partitioning. Fisher proposed an algorithm for the optimum classification,namely the optimum partition method. The basic idea is based on the variance analysis: to look for a partition which can achieve minimum difference between the samples in the same section, and maximum difference between samples in some various sections. This is the optimum partition. Fisher suggests that the variation sections be divided by means of ordered cluster, and the data structure of the number of incidences can be fully taken into account so that the partition can be more reasonable.
Let any kind of variants x1, x2,…, xnbe {xi, xi+1,…,xi}, j > i , i , j = 0,1,2...,n and define the mean vector
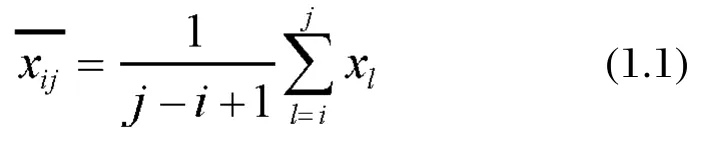
Define the total difference (the index is the sum of squares of deviations)of the samples in one kind as the diameter of that section, denoted as D (i , j):

Divide n sequential variants into k kinds, and any partition can be

Define the error function, namely the objective function of this partition, and let it be the total sum of squares of deviations in this kind:
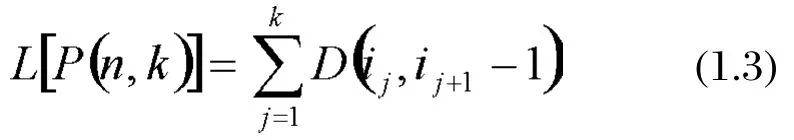
When n and k are fixed, the smaller the error function L[P(n,k)]is, the smaller the sum of squares of deviations within each kind, and this proves the reasonability of the classification. It can be proved that the so-called optimum partition is to make the L[P(n,k)]smallest. k can be calculated according to the relation curve of L[P(n,k)]and k . The value at the turn of the curve is the optimum partition number.
WEIGHTED MARKOV CHAIN
A stochastic process X={X(t),t∈T} is a collection of random variables. That is, for each t in the index set T, X(t)is a random variable. We often interpret t as time and call X(t)the state of the process at time t. If the index set T is a countable set, we call X(t)a discrete-time stochastic process, and if T is a continuum, we call it a continuous-time stochastic process. The collection of possible values of X(t)is called state space. This general model has been described, from a theoretical analysis, by Chiang[30]and others[31].
Markov chain
Markov chain is a branch of Markov process. If the present state of the system is given, then the past and future are (conditionally)independent. Such a behavior is called the Markov property of the system.A Markov chain evolves in a discrete (countable)state space with respect to discrete or continuous time.
A stochastic process X={X(t),t∈T} is defined on a probability space (Ω, F, P), where parameters set T={0,1,2,…} , and state space E={0,1,2,…}. It is called a Markov chain if for any positive integers l,m,k and jl> … > j2> j1(m > jl), im+k,im,ijl,…,ij2,ij1∈E,

For the aperiodic Markov chain, we have

where μjjdenote the mean recurrence time to state j , and πjis the limiting probability. The preceding identity shows that one way to find the limiting probability is by taking the reciprocal of the mean recurrence time. A simple way to find {πi} will be given shortly.
When an irreducible Markov chain is aperiodic and positive recurrent, the chain is called an ergodic Markov chain. The limiting distribution {πj} of an ergodic chain is the unique nonnegative solution of Equations:
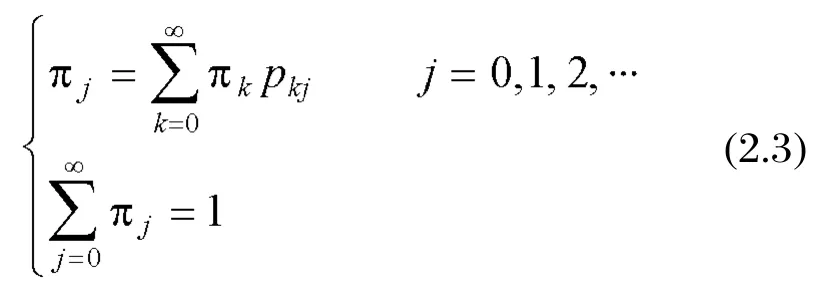
Now πjmay be interpreted as the long-run proportion of time that the Markov chain is in state j .Thus it is easily seen to satisfy (2.2). The solution of these equations, sometimes, is not straightforward, and the MCMC methods may be used to solve them[32],which is considered in the next Section.
There are many properties and relative conclusions about Markov chain, and some other mathematical expressions (e.g., recurrent, limit theorems, periodic,etc.)are described by Freedman[33]and Kendall and Montana[34].
Weighted Markov chain
Because the monthly (or yearly, weekly)incidence of infectious disease are a series of correlative random variables, self-correlation coefficients depict various disease incidence data relationships. The past several months' incidence of infectious disease can be considered in advance to predict the present month incidence data. Then the weighted average can be made according to the incidence of the past several months infectious diseases compared with the present month's. Therefore the prediction purpose to make full and rational use of information is reached. That is the basic thought of weighted Markov chain prediction.
Based on the above discussion in this paper, the specific method of weighted Markov chain prediction is expressed as follows:
① Set up a classification standard of the monthly incidence of infectious disease according to the length of material series and the requirement of the specific problems. For instance, we can classify incidence of infectious disease as one-dimensional sequential cluster analysis in section 2 (corresponding to state space E={1, 2, 3, 4, 5,6})and so on.
② Determine every month's incidence of infectious disease state according to the classification standard of"①".
③ Compute various self-correlation coefficients rk,k∈E,

④ Standardize various self-correlation coefficients.In other words, that is take
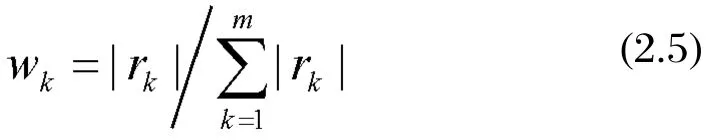
as weights of various (steps)Markov chain (m is the maximum step according to prediction).
⑤ According to statistical results of "②", we can get various steps of Markov chain transition probabilities matrixes, which decided the probability law when incidence of infectious disease states transited.
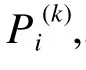
⑦ Take the weighted average of various predicting probabilities of the same state as predicting probability of the plum rains intensity index, that is
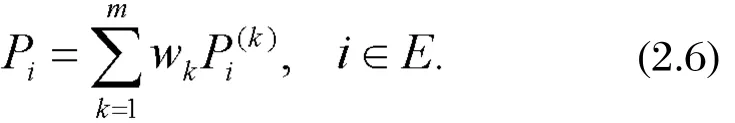
If Pi=max{Pi, i∈E}, i is the predicting state of the present month incidence of infectious disease.After the present month's incidence of infectious disease is determined, we can add it to the original series, repeating steps "①-⑦", and the next month's incidence of infectious disease can be predicted.
⑧The further analysis of Markov chain's characteristics (ergodic property, stationary distribution,etc.)also can be carried out[35,36].
MCMC METHODS
In this section we will describe MCMC methods for the weighted Markov chains. Our approach is analogous to the one used for solving the equations(2.3)in the previous section. Since there has been extensive research conducted and written about MCMC methods, we will be brief[37]. However, it should be noted that the full posterior distribution over all parameters in the model is unwieldy.
One standard method for constructing a Markov chain with the correct limiting distribution is via a recursive simulation of the so-called full conditional densities: that is, the density of a set or block of parameters. Each of the full conditional densities in the simulation is then sampled either directly (if the full conditional density belongs to a known family of distributions)or by utilizing a technique such as the Metropolis-Hastings (M-H)method. An important and crucial point is that these methods do not require knowledge of the intractable normalizing constant of the posterior distribution.
In the present case, we applied MCMC methods to solve the above equations(2.3), iterative and computational details are described in the recent papers of Chib and Winkelmann[38]and Covington et al[39].
APPLICATION
In order to explain specific applications of this method and to conduct testing, this research is based on the samples of the monthly surveillance data of Hepatitis B patients in the period of January 1980 to October 2006 in Jiangsu Province. The weighted Markov chain theory was used to make a forecast and other related analysis of the incidents of the disease in November and February 2000.
Liver cancer is one of the most life-threatening cancers, and is the third-leading cause of death from cancer in China, and the top leading cause in the Province of Jiangsu. There are some 260,000 new cases of liver cancer each year throughout the world. Of all these cancer sufferers, about 42.5%are from China, and 90% of all liver cancer patients have previously been infected by Hepatitis B virus(HBV). A collection of data we gathered and analyzed suggests that about 25% of all those infected with HBV will eventually die of chronic severe hepatitis,cirrhosis of liver and liver cancer. Moreover, both acute and chronic Hepatitis B patients are the main source of infection for HBV. China is densely populated with Hepatitis B patients. According to a nationwide hepatitis epidemiological survey conducted in 2004, the average HBV infection rate of China is 70%-90% (including people infected and being infected). Therefore, the forecasting research of the incidence of HBV has far-reaching implications.
Our forecasting and analysis study is as follows:
① Set up a classification standard of the monthly incidence of infectious disease according to the onedimensional sequential cluster analysis algorithm by SAS 9.1.3 software. The value at the turn of the curve is k = 4 (see, e.g., Fig. 1).
② As Table 1 shows, the incidence data of infectious disease can be classified into 6 grades(corresponding to 4 states of weighted Markov chain),so various months' incidence of infectious disease states can be determined.
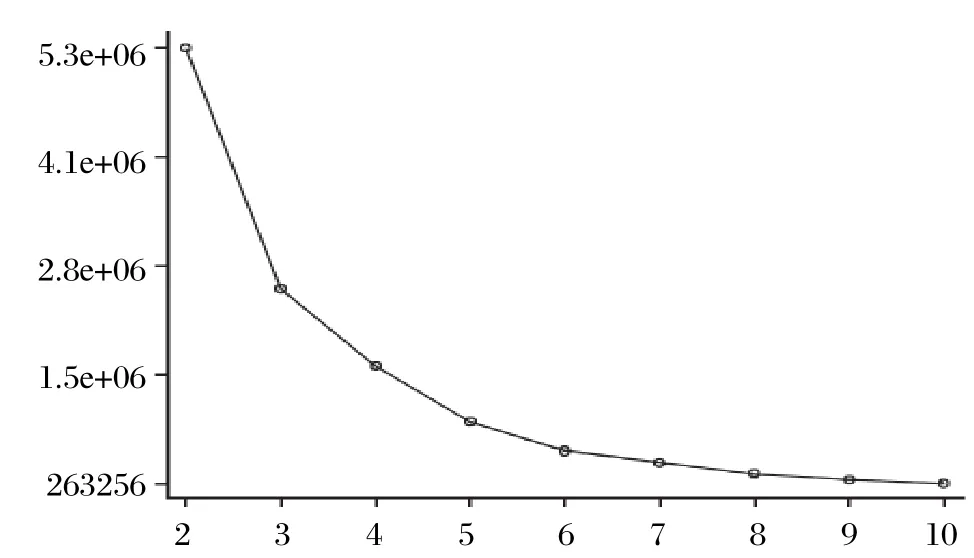
Fig. 1 L[P(n, k)]~k curve
③ According to the Table 1 classification standard,various self-correlation coefficients and Markov chain weights of various steps can be computed (Table 2).

Table 1 Classification of incidence of infectious disease for Jiangsu Province
④ After statistical computation, various one-step transition probabilities matrices with step's length 1, 2,3, 4, 5 and 6 respectively were constructed:
⑤ We took the infectious disease incidence of July 1999 - Dec 1999's series to predict the Jan 2000's infectious disease incidence state. The results are shown below in Table 3.

Table 2 The weights of various steps Markov chain and various self-correlation coefficients

⑥ As Table 3 shows, max{Pi, i∈E} = 0.3734, then i = 3, and the infectious disease incidence state of Jan 2000 is 3. Corresponding infectious disease incidence data x satisfies: 1369 < x ≤ 1641. The actual infectious disease incidence state of Jan 2000 in Jiangsu Province is 1390, and the intensity state is 3. The prediction is correct.
Similarly, the Aug 1999 - Jan 2000 month series can be used to predict the infectious disease incidence state for Feb 2000. This forecasting process is just a repeat of "①-⑤". The prediction results are listed below in Table 4.
⑦ Further analysis of this weighted Markov chain's characteristics can be carried out as in Table 5.
From Table 5, we may infer that the return period of the state j is Tj. The return period of each state will be T1= 17.14(months), T2= 7.5(months), T3=4.14(months), T4= 5(months), T5= 3.43(months),and T6= 13.33(months)respectively. Thus it can be seen that, according to the classifying criteria determined in this article, the state of the number of incidents of Hepatitis B is most probable to appear about 3.43 months per time on average, and at 0.2917 percentage rate. The state 3 is the second, about 4.14 months per time on average, and the percentage is about 0.2417. States 4 and 2 are much less probable than the above; and the state 6 and 1 are least probable to appear, about 13.33 and 17.14 months respectively, with percentages of 0.0750 and 0.0583,respectively.
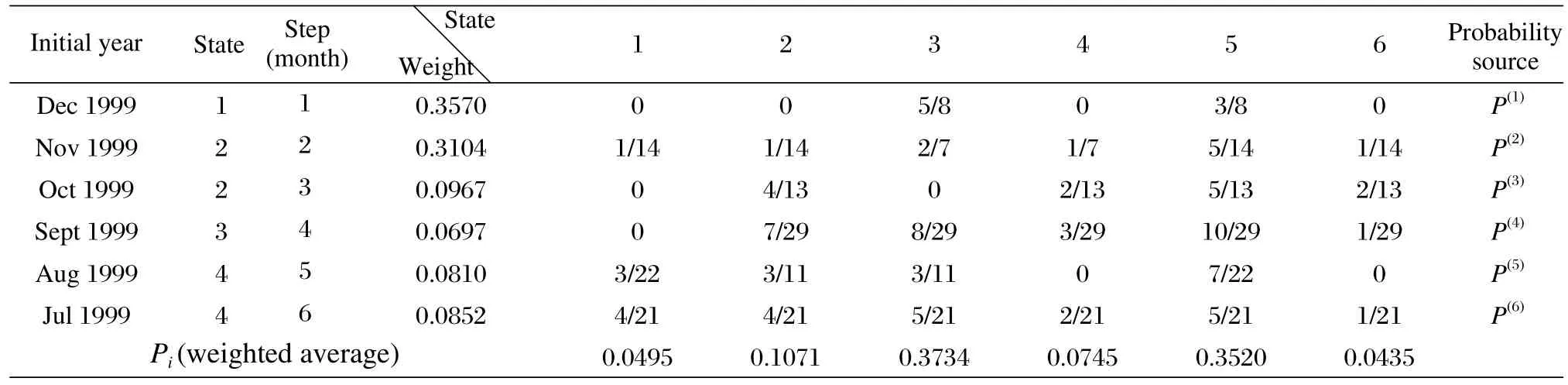
Table 3 Infectious disease incidence state prediction in Jan 2000

Table 4 Infectious disease incidence state prediction in Feb 2000

Table 5. Stationary distribution and recurrence period of various states
CONCLUDING REMARKS
The mathematical statistics tool is an important method for the prediction and forecast of infectious diseases. Historically, forecasting methods such as multivariate statistics analysis, Monte-Carlo simulations, spectrum analysis, that rely heavily on historical data have been used to infer future trends.But the accuracy of these non-subjective forecasting methods needs much improvement. In relation to these non-subjective forecasting methods, the weighted Markov chain theory introduced in this paper has the follow distinguishing characteristics:
① The key to the success of the forecast based on the weighted Markov chain theory in this article is the scientific classification, determination of the initial state of the system, and the ensuring of the state transition probability matrix. In contrast, previous forecasting methods have been heavily reliant on historical data, and largely affected by differences between historical and future environments.
② Since the weighted Markov chain is weighted with autocorrelation coefficient of various steps, the sum of the chain can be used to forecast the number of the infected. Therefore, it is more reasonable and sufficient in using data, and the Markov chain theory and the related analysis are well integrated. In the meantime, to calculate the limit distribution of the sequence applying the ergodic theorem reflects much more information of the sequence of the incidents of the disease in order to make a much more qualitative and quantitative description of the sequence calculated.
③ To determine the classifying criteria applying the ordered cluster, the data structure of the sequence of the patients can be taken full account of in the weighted Markov chain model, and the increase and decline in the historical data will be fully reflected.In this way, we are able to describe the status of the disease more accurately, so as to describe the internal distribution in a more effective way. Various methods in the multivariate statistics and the theory of fuzzy mathematics can be used to classify the state of the samples. The appliers should have a good understanding of the characteristics of the actual data,and accumulate experience in order to find more suitable classifying criteria.
④ With the continual increase of time sequence length, the representativeness of the historical data will be increased accordingly. The autocorrelation coefficient, transition probability matrix and the weight of various steps will change too, and this kind of change is also the process of improvement of the forecast and analysis theory. The forecasting model is not fixed, so the real number of the patients in every period of time should be added to the sequence of historical data. Therefore, the autocorrelation coefficient, transition probability matrix and the weight of the forecast can be adjusted online, and the accuracy of the forecast and analysis will be further improved. Moreover, the epidemic report of the disease forecast should have the same criteria in order to minimize the error and failure of reporting, and the disease information should be accumulated in the real practice.
⑤ With the development of the omy and culture,the improvement of hygiene conditions, and the strengthening of the prevention and control of epidemic diseases by the government, the epidemic diseases are controlled effectively, and the number of patients is declining year after year in China. In determining the structure of the model, all these changes should be paid attention to in order to make the statistical model more consistent with the life environment. Furthermore, as the number of the patients is able to reflect the change of the population and developing trend of the disease when the total population does not fluctuate too much, the paper applies the number of the patients to predict the future condition of the incidents of Hepatitis B in the coming year.
⑥ This forecasting method is effective when the spread and the prevention and control measures have not changed fundamentally. However, if preconditions are not met, the forecast will lose its value. Meanwhile, it is still challenging to calculate the actual number of the incidents of patients based on the state percentage calculated. It is very practical to see the occurrence and development of an epidemic disease as a stochastic process. The forecast and analysis method put forward in this article organically combines stochastic process theory, correlative analysis, ordered cluster analysis and epidemiology.Using an easy calculation and clear concepts, it provides a very good way to explore and discuss the forecast and prediction of epidemic diseases.
[1]Ross SM. Stochastic Processes. John Wiley& Sons,Inc.,NewYork 1991.
[2]Bharucha-Reid AT. Elements of the Theory of Markov Processes and Their Applications. McGraw-Hill Book Company, Inc. 1960.
[3]Lange K. Numerical Analysis for Statisticians. Springer-Verlag, Inc.1999.
[4]Crommelin DT, Vanden-Eijnden E. Fitting time series by continuous-time Markov chains: A quadratic programming approach. J Computational Physics 2006;217:782-805.
[5]Serva M, Fulco UL, Gléria IM, Lyra ML, Petroni F,Viswanathan GM . A Markov model of financial returns.Physica A 2006;363:393-403.
[6]Takahashi K, Morikawa K, Myreshka, Takeda D,Mizuno A. Inventory control for a MARKOVIAN remanufacturing system with stochastic decomposition process. Int J Production Economics 2007;108:416-25
[7]Deslauriers A, L'Ecuyer P, Pichitlamken J, Ingolfsson A,Avramidis AN. Markov chain models of a telephone call center with call blending. Computers Operations Res 2007;34:1616-45.
[8]Chan GK, Asgarpoor S. Optimum maintenance policy with Markov processes. Electric Power Systems Res 2006;76:452-6.
[9]Jaskiewicz A, Nowak AS. On the optimality equation for average cost Markov control processes with Feller transition probabilities. J Math Anal Appl 2006;316:495-509.
[10]Lee H, Chen S. Why use Markov-switching models in exchange rate prediction. Economic Modelling 2006;23:662-8.
[11]Silos P. Assessing Markov chain approximations: A minimal econometric approach. J Econom Dynamics Control 2006;30:1063-79.
[12]Mode CJ, Sleeman CK. Stochastic Processes in Epidemiology. World Scientific, Singapore 2004.
[13]Zhou Y, Shao Y, Ruan Y, Xu J, Ma Z, Mei C et al.Modeling and prediction of HIV in China: Transmission rates structured by infection ages. Mathematical Biosci Engineer 2008;5:403-18.
[14]Yakowitz S, Blount M, Gani J. Computing marginal expectations for large compartmentalized models with application to AIDS evolution in a prison system. J Mathematics Appl Med Biol 1996;13:223-44.
[15]Zhang W, Chaloner K, Cowles MK, Zhang Y, Stapleton JT. A Bayesian analysis of doubly censored data using a hierarchical Cox model. Statist. Med 2008;27:529-42.
[16]Islam M A. Multistate survival models for transitions and reverse transitions: an application to contraceptive use date. J Roy Statistical Society A 1994; 157: 441-55.
[17]Janardan KG. On a distribution associated with a stochastic process in Ecology. Biomet J 2002;44:510-22.
[18]Boher JM, Pujol JL, Grenier J, Daurès JP. Markov model and markers of small cell lung cancer: Assessing the influence of reversible serum NSE, CYFRA 21-1 and TPS levels on prognosis. Brit J Cancer 1999;79:1419-27.
[19]Trajstman AC. A Markov chain model for Newcastle disease and its relevance to the intracerebral pathogenicity index. Biomet J 2002;44:43-57.
[20]Wang P, Puterman ML. Analysis of longitudinal data of epileptic seizure counts: A two state hidden Markov regression approach. Biomet J 2001;43:941-62.
[21]Hendriks JC, Craib KJ, Veugelers PJ, Van Druten HA,Coutinho RA, Schechter MT, et al. Secular trends in the survival of HIV-infected homosexual men in Amsterdam and Vancouver estimated from a death-included CD4-staged Markov model. Int J Epidemiol 2000; 29:565-72.
[22]Sommen C, Alioum1 A, Commenges D. A multistate approach for estimating the incidence of human immunodeficiency virus by using HIV and AIDS French surveillance data. Statist. Med 2009; 28:1554-68.
[23]Becker NG. Analysis of Infectious Disease Data.Chapman and Hall, London & New York 1942.
[24]Volz E, Meyers LA. Epidemic thresholds in dynamic contact networks. J Roy Soc, Interface/the Royal Society 2009;6:233-41.
[25]Kretzschmar M, Jager JC, Reinking DP, Van Zessen G, Brouwers H. The basic reproduction ratio R0 for a sexually transmitted disease in a pair formation model with two types of pairs. Math Biosci 1994;124:181-205.
[26]Johnson DE. Applied Multivariate Methods for Data Analysts. Higher Education Press, Beijing 2005.
[27]DeRisi JL, Iyer VR, Brown PQ. Exploring the metabolic and genetic control of gene expression on a genomic scale. Science 1997;278:680-6.
[28]Lander ES. Array of hope. Nature Genet 1999;21:3-4.
[29]Quackenbush J. Computational analysis of microarray data. Nat Rev Genet 2001;2:418-427.
[30]Chiang CL. An Introduction to Stochastic Processes and their Application. Robert E. Krieger Publishing Company, New York 1980.
[31]Iseacson DL, Madsen RW. Markov Chains Theory and Applications, John Wiley and Sons, Inc., NewYork 1976.
[32]Lu Y, Fang J. Advanced Medical Statistics. World Scientific, Singapore 2003.
[33]Freedman D. Markov Chains. Springer-Verlag 1983.
[34]Kendall WS, Montana G. Small sets and Markov transition densities. Stochastic Processes and their Applications 2002;99:177-94.
[35]Bartlett MS. Measles periodicity and community size. J Roy Statistical Soc 1957;120:48-70.
[36]Mitavskiy B, Cannings C. Estimating the ratios of the stationary distribution values for Markov chains modeling evolutionary algorithms. Evolutionary Computation 2009;17:343-77.
[37]Heffernan JM, Wahl LM. Natural variation in HIV infection: Monte Carlo estimates that include CD8 effector cells. J Theoret Biol 2006;243:191-204.
[38]Chib S, Winkelmann R. Markov chain Monte Carlo analysis of correlated count data. J Business Econc Statistics 2001;19:428-35.
[39]Covington TR, Robinan Gentry P, Van Landingham CB, Anderson ME, Kester JE, Clewell HJ. The use of Markov chain Monte Carlo uncertainty analysis to support a Public Health Goal for perchloroethylene. Reg Toxicol Pharmacol 2007;47:1-18.
 THE JOURNAL OF BIOMEDICAL RESEARCH2010年3期
THE JOURNAL OF BIOMEDICAL RESEARCH2010年3期
- THE JOURNAL OF BIOMEDICAL RESEARCH的其它文章
- HGF percutaneous endocardial injection induces cardiomyocyte proliferation and rescues cardiac function in pigs☆
- CYP17 T27C polymorphism and prostate cancer risk:a meta-analysis based on 31 studies
- RNAi knockdown of C-erbB2 expression inhibits salivary gland adenoid cystic carcinoma SACC-83 cell growth in vitro
- Elevated expression of mature miR-21 and miR-155 in cancerous gastric tissues from Chinese patients with gastric cancer
- Identification of the metabolites of polybrominated diphenyl ether 99 and its related cytochrome P450s☆
- Effects of heme precursors on CYP1A2 and POR expression in the baculovirus/Spodoptera frugiperda system☆
